In routine research, we often use statistical probability concepts to support urban studies. Therefore, mastering statistical probability topics is necessary. This article discusses commonly encountered probability distributions and aims to provide a conceptual overview.
1. Random variables
All possible outcomes of a random experiment are random variables. A set of random variables is denoted by X. If the possible outcomes are countable, the variable is called a discrete random variable. For example, if you flip a coin 10 times, the number of heads can be represented by an integer. The number of apples in a basket is also countable.
Continuous random variable
These are values that cannot be represented discretely. For example, a person might be 1.7 m tall, 1.80 m tall, 1.6666666... m tall, and so on.
2. Density functions
We use density functions to describe the probability distribution of a random variable X.
PMF: probability mass function
The PMF returns the probability that a discrete random variable X equals x. The sum over all possible values equals 1. The PMF applies only to discrete variables.
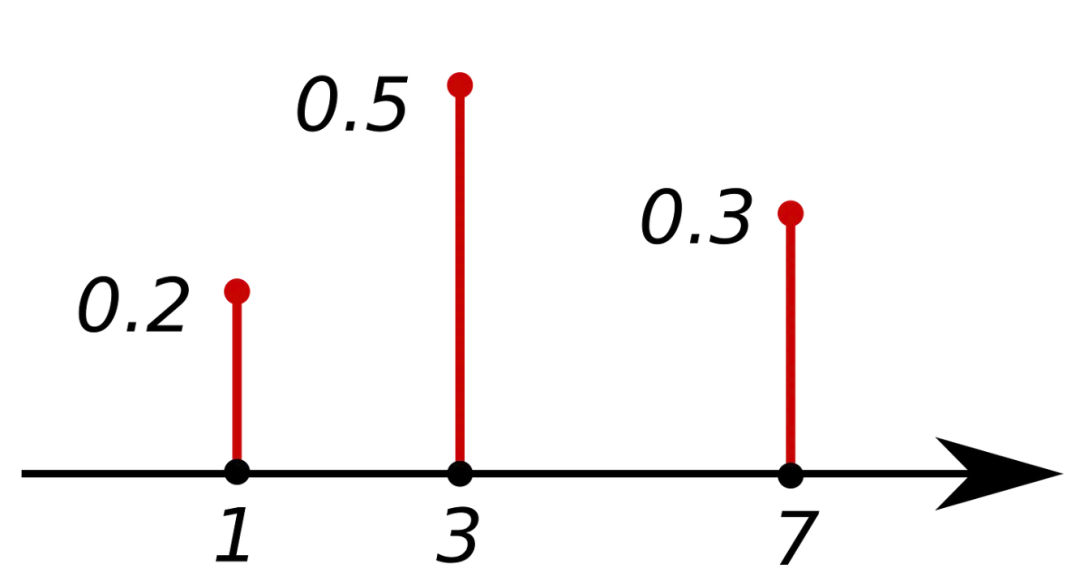
PMF. Source: Wikipedia
PDF: probability density function
The PDF is the continuous-variable counterpart to the PMF. It gives the probability for a continuous random variable X to fall within a given range.
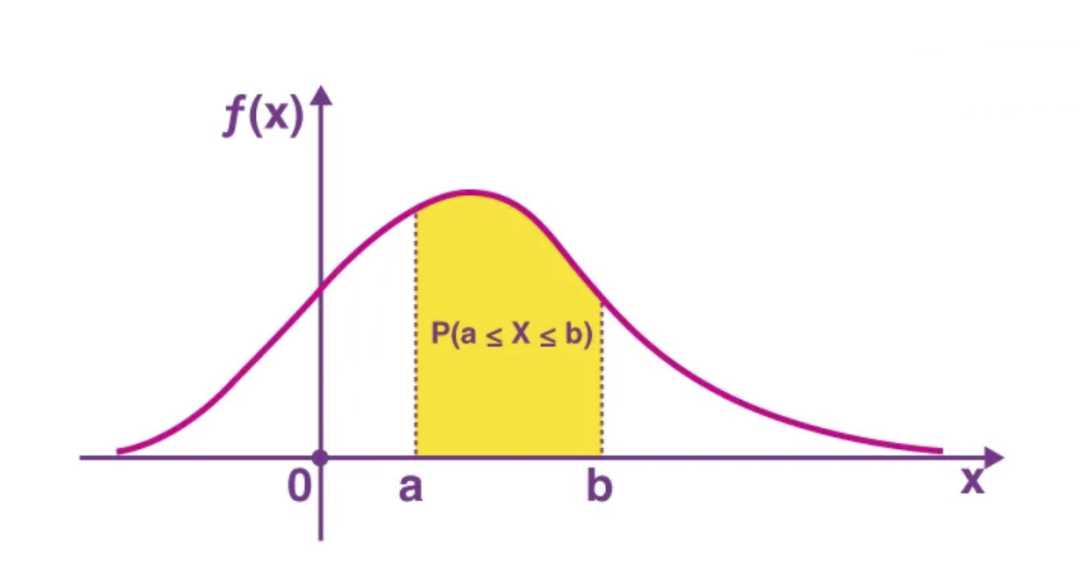
PDF. Source: Byjus
CDF: cumulative distribution function
The CDF returns the probability that a random variable X takes a value less than or equal to x.
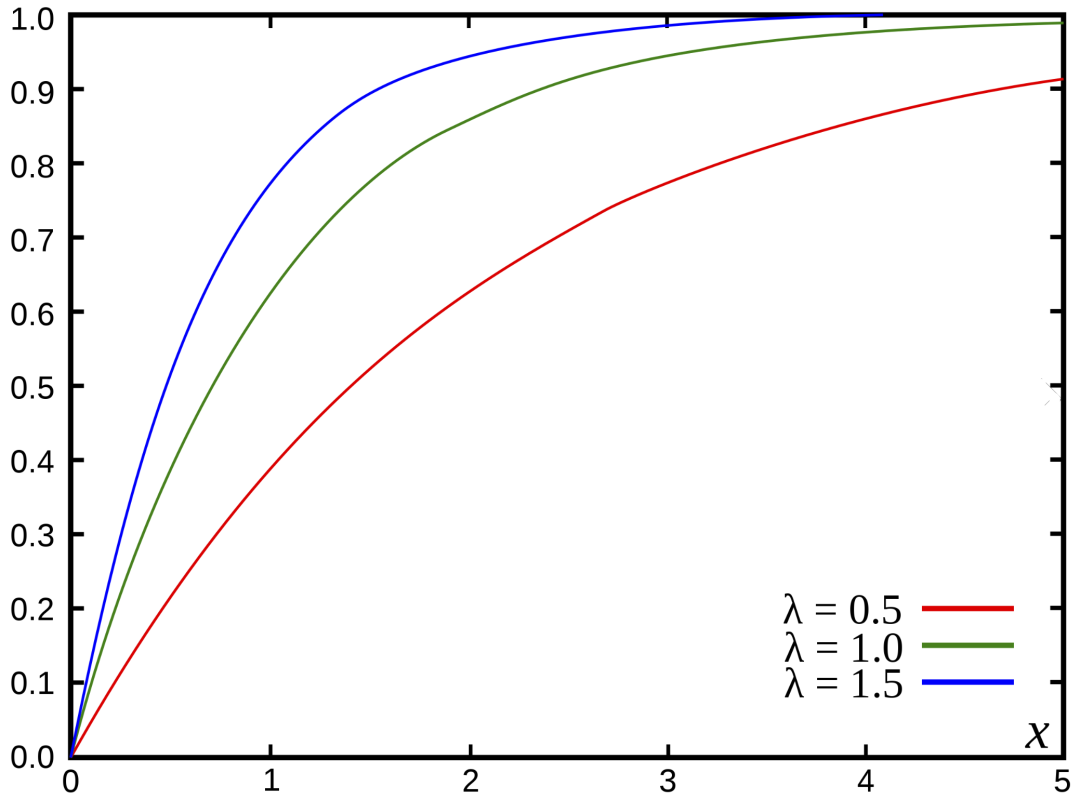
CDF (cumulative distribution function of the exponential distribution). Source: Wikipedia
3. Discrete distributions
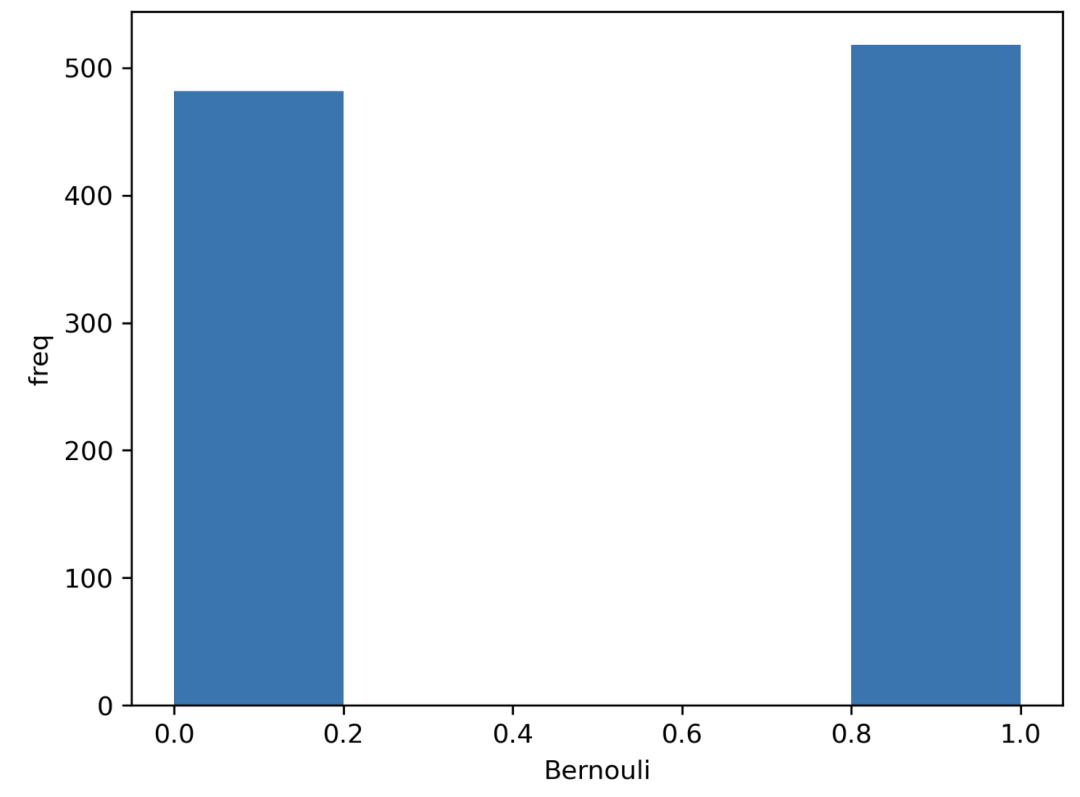
Bernoulli distribution
We have a single trial (one observation) with two possible outcomes, for example a coin toss. We have a true (1) result and a false (0) result. Assume heads corresponds to true (success). If the probability of heads is p, the complementary probability is 1-p.
import seaborn as sns from scipy.stats import bernoulli # Single observation # Generate data (1000 points, possible outs: 1 or 0, probability: 50% for each) data = bernoulli.rvs(size=1000,p=0.5) # Plot ax = sns.distplot(data_bern,kde=False,hist_kws={"linewidth": 10,'alpha':1}) ax.set(xlabel='Bernouli', ylabel='freq')
 ALLPCB
ALLPCB