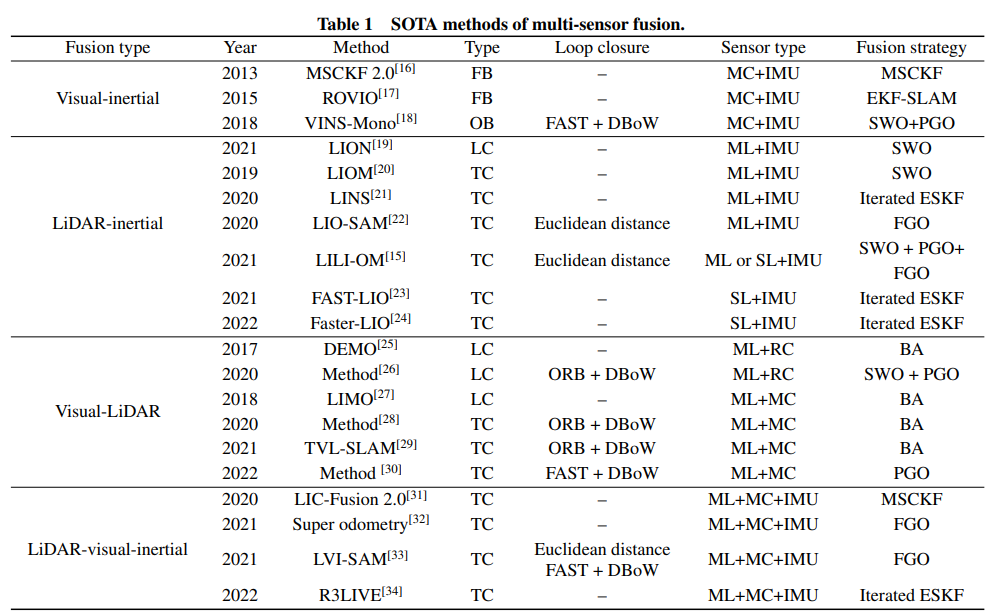
1. Basic operating principle of optical fiber sensors
The structure and principle of a fiber Mach-Zehnder interferometer are shown in the figure above. Light from the source passes through coupler DC1 and is split into two beams. One fiber arm serves as the signal arm and the other as the reference arm. The beams recombine at coupler DC2 and interfere; the interference light falls on a detector. The resulting optical intensity expressions are given below.
2. Mach-Zehnder fiber temperature sensor principle
A laser beam emitted from the laser is split by a beam splitter and launched into two optical fibers of nearly identical length. The outputs of the two fibers are then combined to produce interference, generating interference fringes. When the temperature of one fiber arm changes relative to the other, the phase difference of the light transmitted in the two fibers changes, causing the interference fringes to shift. The number of fringe shifts reflects the change in the measured temperature. A photodetector receives the fringe variations and sends the signals to an appropriate data-processing system to obtain the measurement result.
3. Mach-Zehnder fiber pressure sensor principle
Laser light from a He-Ne laser is coupled into an optical coupler and split into two beams transmitted through fibers L1 and L2, respectively. The outputs of the terminal coupler form interference fringes. The optical path of fiber L1 remains constant, while the optical path of fiber L2 changes with pressure. When pressure increases, the optical path increases; when pressure decreases, the optical path decreases. Let the optical path difference be δ. The phase difference ΔΦ caused by this optical path difference is
where λ is the laser wavelength, P is the pressure, and S is the conversion coefficient of the pressure-sensing fiber (related to the sensing fiber's length, refractive index, and cross-sectional area variation).
The interference fringe intensity I relates to the phase difference ΔΦ as follows:
where I0 is the average optical intensity and K is the fringe contrast.
Each time the optical path difference δ changes by one wavelength λ, i.e., when the pressure changes by ΔP = λ / S, the interference fringes alternate between bright and dark once; the intensity variation is approximately sinusoidal. If the number of bright-dark fringe changes is N, then the pressure change is
 ALLPCB
ALLPCB