Abstract
This survey examines the motivations, challenges, background, recent advances, and the relationship between deep learning and metric learning. It details problem formulations, sample selection strategies, metric loss functions, current status, and future directions of deep metric learning.
1. Introduction
Machine learning is widely applied across fields such as face recognition and medical diagnosis, addressing complex problems and large datasets. Learning algorithms can produce effective classification models from data, but each dataset presents specific challenges that require discriminative features for correct classification. Common algorithms include k-nearest neighbors, support vector machines, and naive Bayes classifiers, which may require feature weighting and data transformation.
Metric learning is a subfield of machine learning focused on learning similarity or distance measures between samples in a dataset. It plays a key role in tasks that require comparison and discrimination among samples.
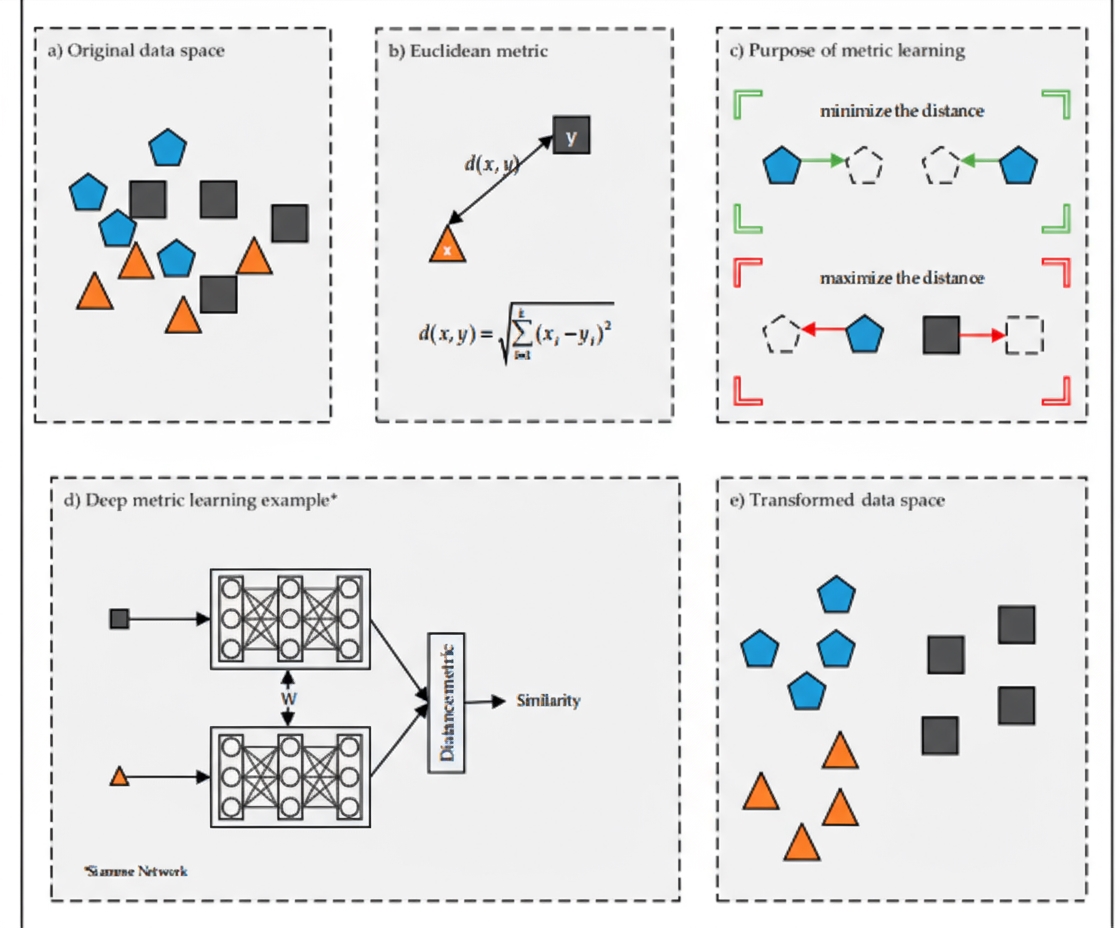
Deep learning provides new data representations that automatically extract features, including nonlinear structures. Combining deep learning and metric learning yields deep metric learning (see Figure 1), which is grounded in sample similarity principles. Network architecture, loss functions, and sample selection are critical to the success of deep metric learning.
This survey explores the significance and challenges of deep metric learning, summarizes background and recent improvements, and explains problem formulations, sample selection, and metric loss functions, while outlining the current state and future directions.
2. Metric Learning
Each dataset has specific challenges for classification and clustering, and a proper distance metric is essential for good results. Metric learning methods derive new distance metrics by analyzing data, improving discriminability. The main objective is to learn a metric that reduces distances among samples from the same class and increases distances among samples from different classes, creating larger margins between classes and improving classification and clustering performance (see Figure 1c).
Metric learning in the literature is directly related to the Mahalanobis distance.
dM(xi, xj) is a distance measure that must satisfy non-negativity, identity of indiscernibles, symmetry, and the triangle inequality. M must be symmetric and positive semidefinite, with nonnegative eigenvalues or determinant, and can be decomposed as:
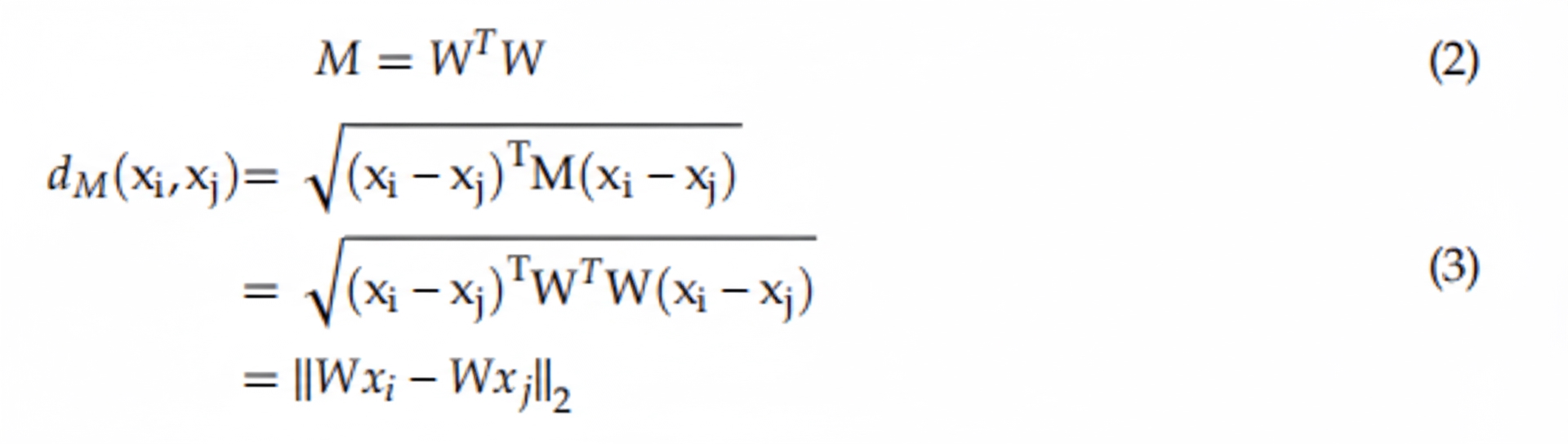
From this decomposition, W represents a linear transformation. The Euclidean distance between two samples in the transformed space equals the Mahalanobis distance in the original space. This linear transform underlies metric learning formulations.
Better data representations enable more accurate classification and clustering. Metric learning provides meaningful representations by learning effective distance metrics. Linear metric learning methods offer flexible constraints in transformed spaces and can improve learning performance, but they struggle to capture nonlinear features. Kernel methods map data into nonlinear spaces to improve performance but can cause overfitting. Deep metric learning offers a more compact solution that addresses limitations of linear and kernel-based methods.
3. Deep Metric Learning
Traditional machine learning relied on feature engineering, preprocessing, and handcrafted feature extraction, requiring domain expertise. Deep learning learns hierarchical representations directly within classification architectures. Deep models need large datasets and can perform poorly with limited data, in addition to long training times. GPU acceleration libraries such as cuDNN have enabled high-performance training of deep neural networks.
Common predefined similarity measures include Euclidean, Mahalanobis, Matusita, Bhattacharyya, and Kullback-Leibler distances, but these metrics may be limited for classification. Mahalanobis-based approaches transform data into more discriminative feature spaces; however, they may not capture underlying nonlinear structure. Deep learning addresses this by using nonlinear activation functions and deep architectures.
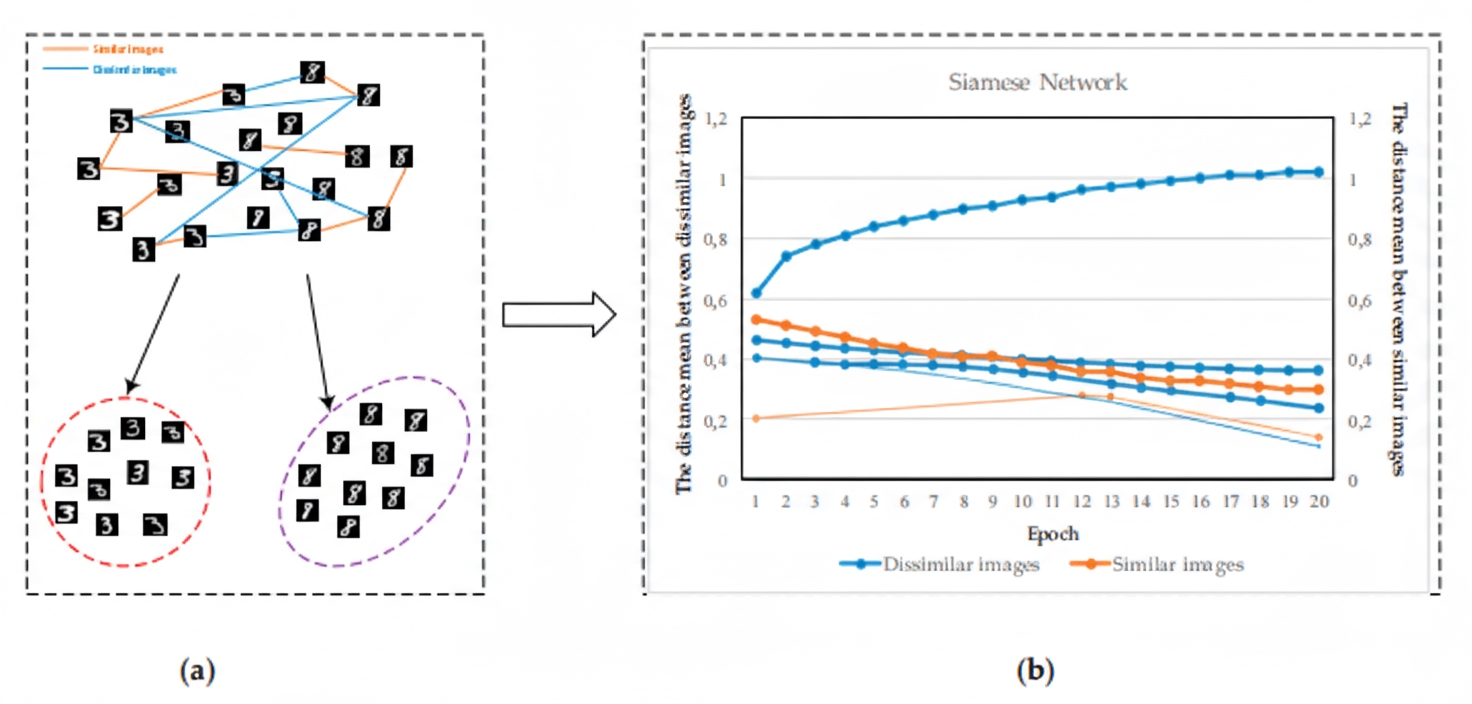
Distance-based approaches have gained interest in deep learning. Deep metric learning aims to minimize distances among similar samples and maximize distances among dissimilar samples, directly shaping the learned embedding. Metric loss functions benefit deep networks by enforcing these distances. By pulling samples of the same class closer and pushing samples of different classes apart (see Figure 2), deep metric learning improves discrimination. Experiments on MNIST with contrastive loss demonstrate effectiveness in this setting.
3.1 Problem Domains for Deep Metric Learning
Deep metric learning learns nonlinear subspace similarities via deep architectures and is applied to many domains, including video understanding, person re-identification, medical imaging, 3D modeling, face verification and recognition, and signature verification.
Video understanding
Video understanding tasks such as annotation, recommendation, and search can benefit from metric-based solutions. For example, models that extract audio and visual features and then learn embeddings via triplet-based deep networks can improve localization in surveillance. Distance-based methods have also been used for visual tracking, showing advantages of operating in metric spaces.
Person re-identification
Person re-identification aims to identify the same person across different camera views. Deep metric learning enables end-to-end learning of embeddings that map input images to discriminative feature spaces. Models often use paired convolution and pooling layers, computing cross-input neighborhood differences and combining patch-sum attributes and softmax to determine whether images depict the same person. Improvements include refined triplet generation strategies and optimized gradient descent for triplet loss.
Medical imaging
Deep learning addresses classification, detection, segmentation, and registration in medical imaging. Deep metric learning improves data representation through similarity-based methods, helping distinguish normal from abnormal images. Losses that consider global embedding structure and overlapping labels, such as ML2, provide higher-level representations for medical image analysis.
3D modeling
Deep metric learning performs well in 3D shape retrieval. Shared-weight networks and metric losses improve retrieval for both sketches and 3D shapes. CNN plus Siamese architectures achieve efficient 3D image retrieval on large datasets by combining correlation and discriminative losses. Hidden layers can also be trained with metric loss. Novel losses combining triplet and center losses have been proposed for 3D tasks, and triplet networks are used to capture style-related similarity.
Face verification and recognition
Deep metric learning has driven advances in face verification and recognition. Hierarchical nonlinear transform models and systems using online triplet mining focus on Euclidean-space face embeddings for verification, recognition, and clustering. Related tasks include expression recognition and age estimation.
Text and information retrieval
Deep metric learning is applied to text similarity and retrieval. Siamese networks can capture semantic similarity between sentences. Models using regression-based training, dependency-aware Siamese LSTM, and weakly supervised triplet generation for sentence embeddings have been explored for clustering and retrieval tasks.
Audio and speaker recognition
Triplet and quadruplet networks are used for speaker embedding and verification. Sampling strategies and margin parameters affect performance. Semi-hard negative mining, effective in vision, may only work under specific settings for speaker tasks. Prototype network losses and triplet losses have both shown success in speaker verification and identification, with prototype losses offering faster training and competitive performance.
Deep metric learning has also been applied to music similarity, crowd counting regression, similar region search, volumetric image recognition, instance segmentation, edge detection, and pansharpening. The volume of academic publications reflects growing interest in the field (see Figure 3).
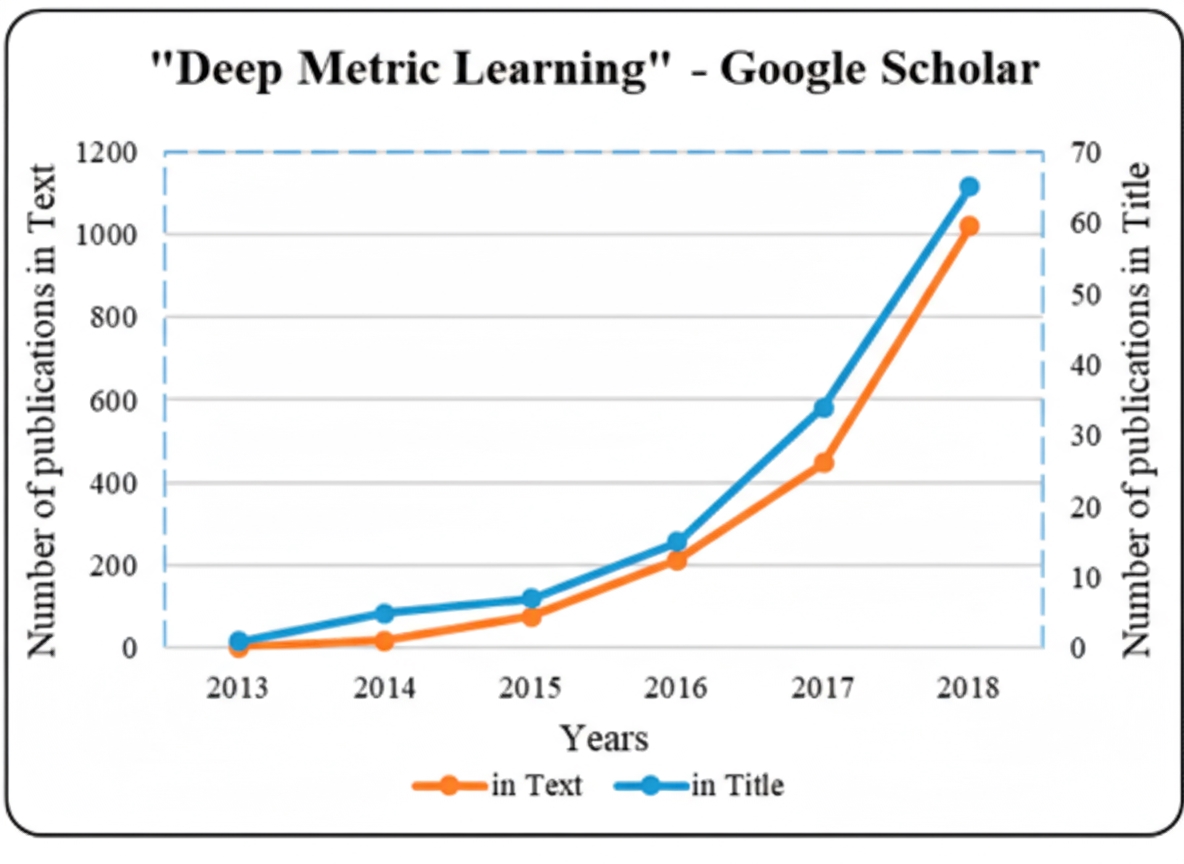
3.2 Sample Selection
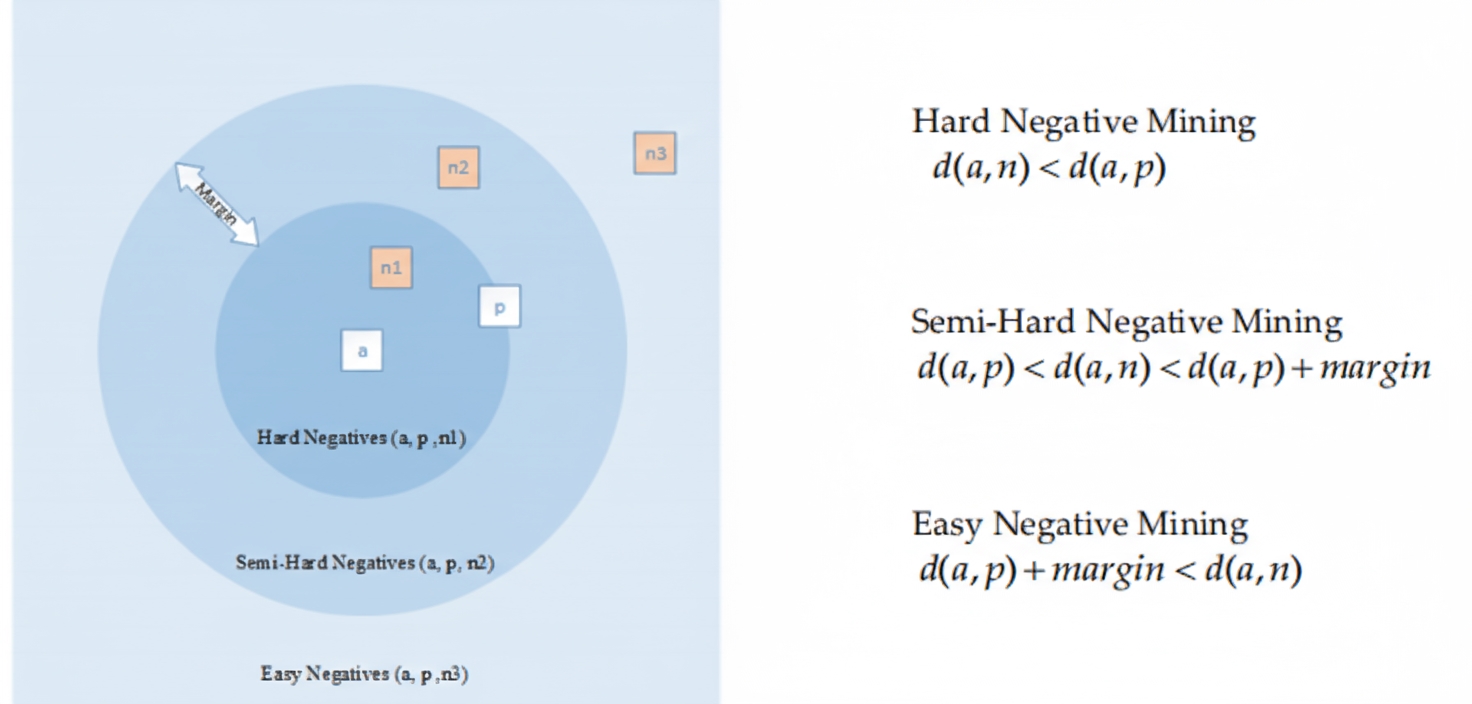
Deep metric learning involves input samples, network architecture, and metric loss functions. Sample selection critically affects classification performance and training speed. Random selection of positive and negative pairs is the simplest approach for contrastive loss but may slow learning once performance improves. Hard negative mining and triplet mining can boost performance, but naive triplet sampling can be ineffective. Informative triplets provide better training signals.
Hard negatives are false-positive samples; semi-hard negative mining finds negatives within decision boundaries but farther from the anchor than hard negatives. Triplet mining selects negatives based on distances among anchor, positive, and negative samples (see Figure 4). Negatives too close to the anchor produce high gradient variance and low signal-to-noise ratio; distance-weighted sampling can mitigate noisy samples. Negative class mining selects one sample per class as negatives for the triplet network and can use greedy search to choose multiple negatives.
Even with sound mathematical models and architectures, a network's learning capacity is limited by the discriminative power of training samples. Presenting the network with discriminative examples improves representation learning. Sample selection as a preprocessing strategy can enhance model performance. Research on negative mining in deep metric learning has high impact value: selecting informative samples can prevent overfitting, accelerate learning, and reduce resource waste, leading to substantial performance gains.
3.3 Metric Loss Functions
This section summarizes loss functions used in deep metric learning, describing their usage and differences. These losses optimize feature representations by shaping object similarity.
Siamese networks were initially applied to signature verification within an energy-based discriminative learning framework. The network takes paired inputs and learns a binary outcome indicating whether the inputs belong to the same class. Contrastive loss benefits Siamese networks and inspired further research in deep metric learning. Siamese architectures can maximize or minimize distances between objects to improve classification. Weight sharing helps extract meaningful patterns, and Siamese networks combined with convolutional networks can learn similarity from raw pixels, color, and texture. Deep metric models have combined twin CNNs with Mahalanobis-like metrics for person re-identification (see Figure 5).
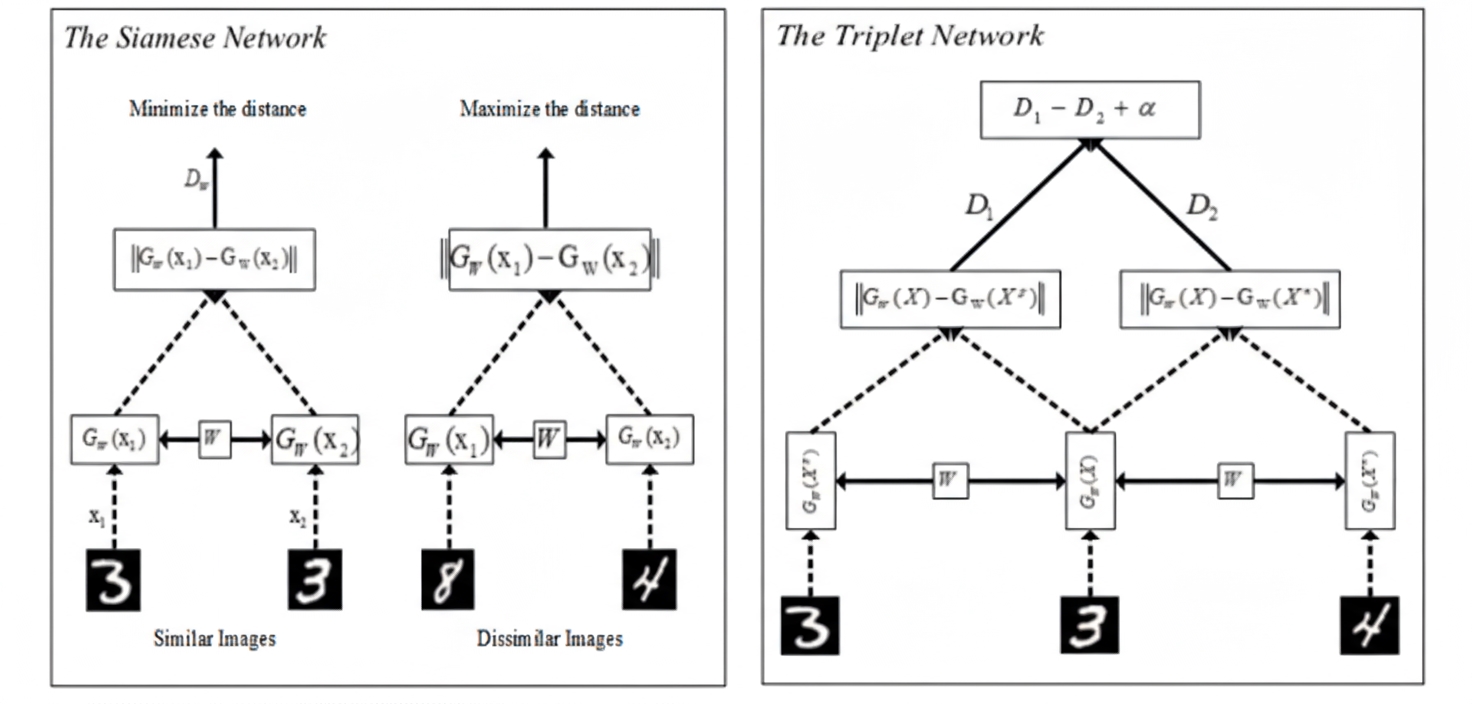
Triplet networks extend Siamese ideas with three inputs: anchor, positive, and negative. Triplet loss compares distances in Euclidean space to enforce that the anchor is closer to the positive than to the negative (see Figure 6). Triplet networks exploit both within-class and between-class relationships, offering stronger discrimination. Variants include hierarchical triplet loss with online adaptive tree updates and angular loss, which constrains angles in the triplet triangle to push negatives away from the positive cluster center while bringing positives closer together; angular measures are rotation- and scale-invariant. Quadruplet loss uses four samples per training batch for improved separation. Histogram loss trains with quadruplets to model positive and negative similarity distributions without parameter tuning and has shown strong results in person re-identification. Part-based losses evaluate different body parts by splitting images and computing per-part loss values.
where Xc lies between X and X_p. Xc is defined as:
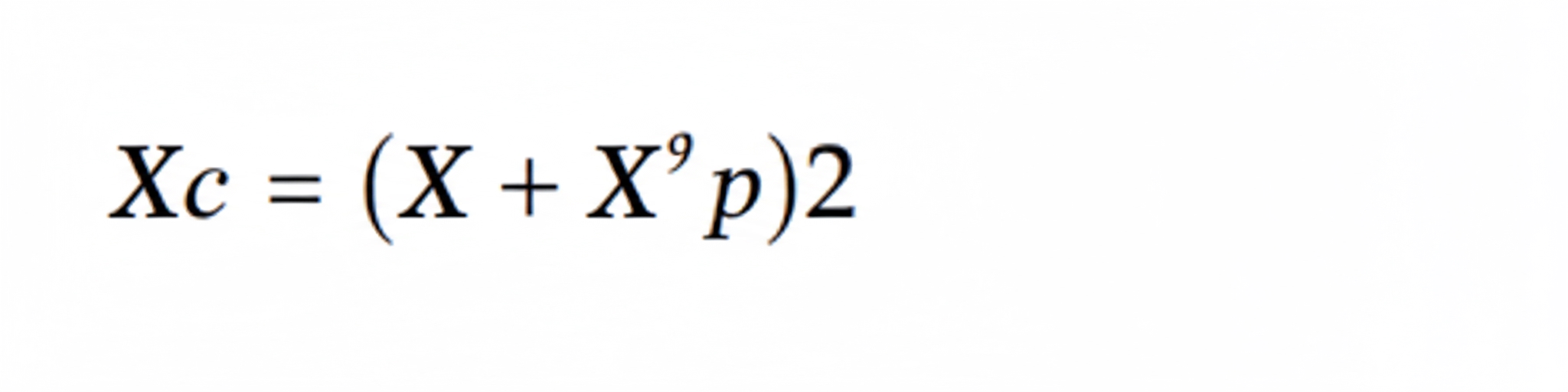
Conventional deep metric structures such as Siamese and triplet networks may ignore structural information among training samples. Structured deep metric learning elevates pairwise distance vectors to pairwise distance matrices through specialized structured losses, leveraging contextual information. Sohn proposed N-pair loss to address slow convergence and local optima in Siamese and triplet networks. N-pair loss benefits from N-1 negative class samples for comparison with the anchor (see Figure 6e). Multi-similarity loss simultaneously considers self-similarity and relative similarity to more effectively collect and weight informative sample pairs.
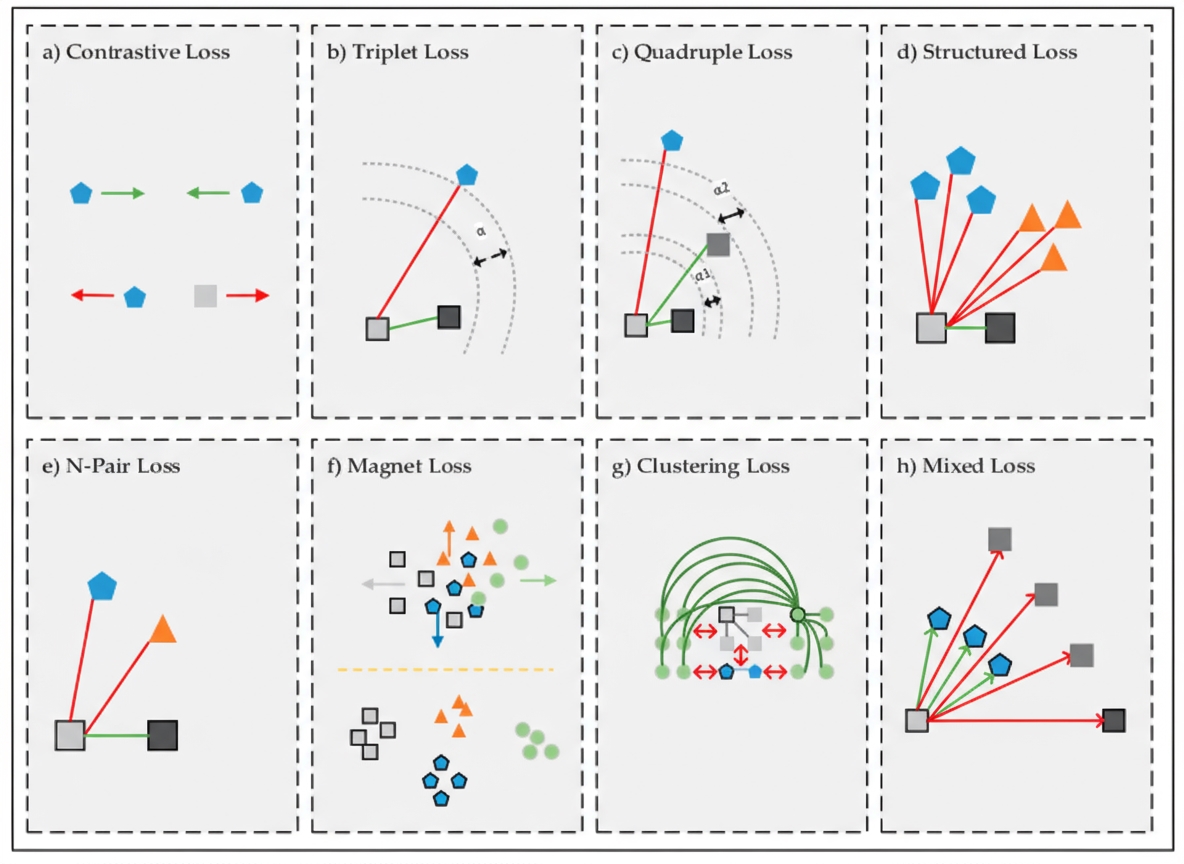
Preparing training data for Siamese, triplet, and N-pair networks requires more disk space and time. Cluster-based losses can group samples into clusters to prevent different clusters from approaching each other. Triplet loss evaluates one triplet at a time, which reduces learning throughput and can lead to insufficient training. Magnet loss addresses cluster overlap by penalizing overlaps and evaluating nearest neighbors within clusters, providing local discrimination that is globally consistent with the optimization process. Mixed loss variants, inspired by triplet loss, incorporate multiple positive and negative samples per anchor to better model inter-sample similarity. Figure 6h illustrates how using local neighborhoods brings similar samples near the nearest cluster.
4. Discussion
Deep metric learning (DML) is applied to face verification, recognition, person re-identification, and 3D shape retrieval. DML is particularly effective in tasks with many classes and few samples per class. DML comprises metric loss functions, sampling strategies, and network structures such as Siamese, triplet, and quadruplet networks. Losses like contrastive, triplet, quadruplet, and N-pair increase effective training sample size but can lengthen training time and increase memory use. Hard and semi-hard negative mining provide informative samples; appropriate sampling strategies are critical for fast convergence. Cluster-based losses avoid extensive data preparation. DML typically runs on GPUs, though some strategies can scale on CPU clusters for very large batches. DML is highly data-dependent, and metric losses may not guarantee fast convergence. Pretrained network weights can help embeddings converge faster and produce more discriminative representations.
5. Conclusion
Deep metric learning is an active research area that learns similarity metrics to compute similarity or dissimilarity between objects. Siamese and triplet networks have demonstrated effectiveness across image, video, text, and audio tasks. Research in deep metric learning spans input sampling strategies, network architectures, and metric loss functions. Future work includes optimizing sampling strategies, combining shared weights with metric losses, and addressing limitations of current methods, including integrating local and global feature representations.
 ALLPCB
ALLPCB