1. Confusion about convolution
The concept of convolution is often introduced early, but many people feel they never really understood it. Textbooks typically present a definition, list properties, and use examples and diagrams, yet they often do not explain why the operation is designed that way or what the underlying meaning is. For someone with a physics background, a formula without an intuitive, practical explanation of its "physical" meaning feels incomplete.
Textbooks usually define the convolution f * g(n) of functions f and g as follows:
Continuous form:
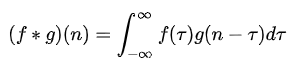
Discrete form:
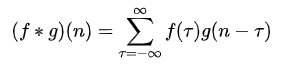
Texts also explain flipping g, which corresponds to folding g from the right to the left on the number line, hence the "convolution" name.
Then g is shifted to n, the corresponding points of the two functions are multiplied and summed; this is the "multiply" part of convolution.
This explains the computational procedure and is mathematically correct, but asking why we flip before shifting and what purpose that serves can still be puzzling.
On online Q&A forums, many contributors have given vivid analogies for convolution, such as rolling a carpet, throwing dice, slapping hands, or saving money. These are lively and interesting, but on closer inspection some parts remain unclear or could be improved. After thinking about the topic for a couple of nights, I reached some conclusions and share them here for discussion. This article focuses on explaining two questions:
- What does the term convolution mean? What does the "fold" mean and what does the "multiply" mean?
- What is the underlying meaning of convolution and how should it be explained?
2. Application scenarios considered
To better understand these questions, consider two typical application scenarios:
- Signal analysis
An input signal f(t) passes through a linear system characterized by a unit impulse response g(t). The output signal is given by the convolution of f and g.
- Image processing
An input image f(x,y) convolved with a designed kernel g(x,y) produces outputs such as blurring or edge enhancement.
3. Understanding convolution
Interpretation of the term convolution: The convolution of two functions essentially means flipping one function and then performing sliding accumulation.
In the continuous case, accumulation is integration of the product of the two functions; in the discrete case it is a weighted sum. For simplicity, call both cases accumulation.
The overall process can be visualized as:
flip -> slide -> accumulate -> slide -> accumulate -> slide -> accumulate ...
The series of accumulated values obtained from successive slides forms the convolution function.
The "fold" in convolution refers to flipping the function, turning g(t) into g(-t); it also implies the sliding motion (a suggestion credited to a commenter). If convolution were translated as "fold-sum" the character would only capture the flipping aspect.
The "multiply" in convolution refers to integration or weighted summation.
Some explanations emphasize only sliding and summing without mentioning flipping; that is incomplete. Others confuse the meaning of "fold" and "multiply"; that is a misinterpretation.
Meaning of convolution:
- From the "multiply" process we see the accumulated value is a global concept. In signal analysis, the convolution result at time T depends not only on the input at time T but on all past inputs, accounting for the cumulative effect of earlier inputs. In image processing, convolution mixes pixel values in a neighborhood, or even across the image, applying weighted processing to the current pixel. Thus "multiply" represents a global mixing or blending of the two functions in time or space.
- Why flip? Why not just multiply directly? Flipping imposes a constraint: it specifies the reference for accumulation. In signal analysis, flipping defines how contributions from times before and after a reference point are combined. In spatial analysis, it defines which neighborhood around a given location is used for accumulation.
4. Examples
Below are several examples illustrating why flipping is needed and what accumulation means.
Example 1: Image processing
Again following an example from an online Q&A, an image can be represented as a matrix:

A processing function (smoothing or edge detection) can be represented by a matrix g, for example:
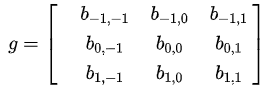
We are now dealing with a two-dimensional function:
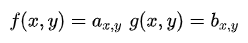
How do we compute the convolution of f and g at (u,v)?
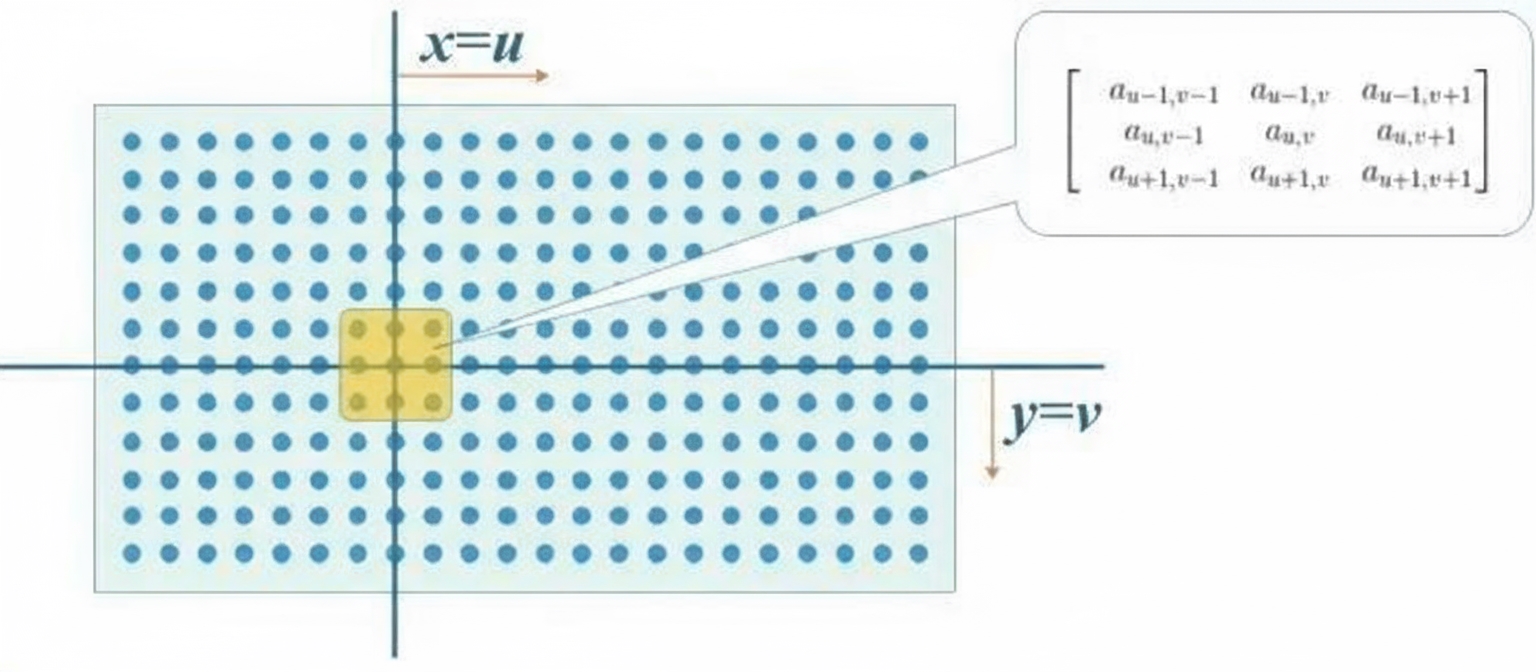
First extract the neighborhood matrix centered at (u,v) from the original image:
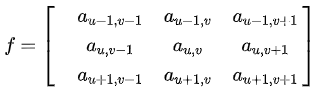
Then flip the processing matrix. This flip is along the diagonal from top-right to bottom-left, not independently along x and y axes; this arrangement fits the inner-product form used below:
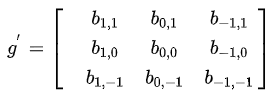
Compare:
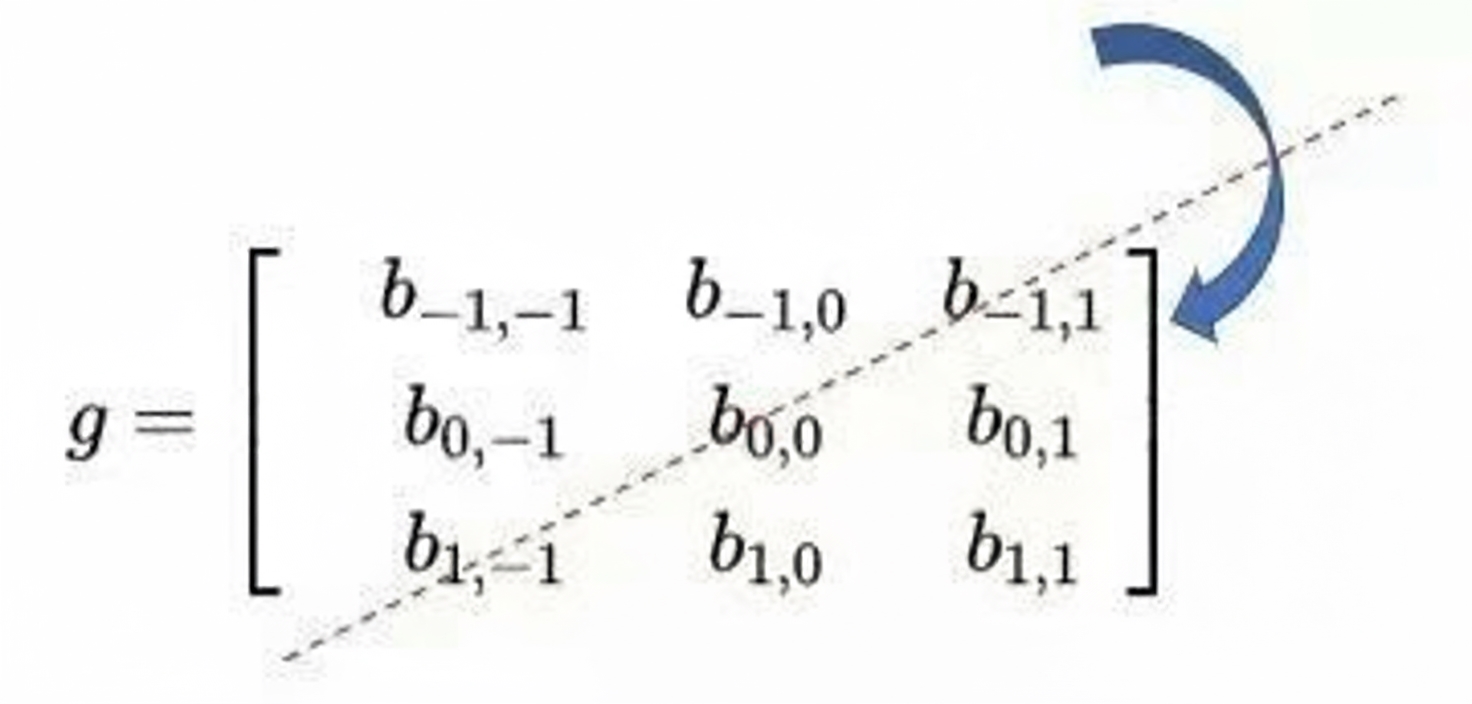
Convolution at (u,v) can be computed as the inner product:
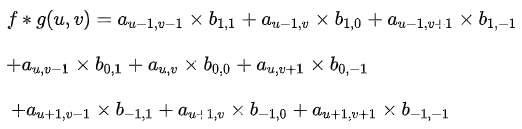
Note that in this formula the subscripts of the multiplied elements a and b sum to (u,v). This enforces the constraint for the weighted sum and explains why g is flipped. The flipped matrix is used for direct inner-product calculation.
The calculation above gives the convolution at (u,v). By sliding along the x and y axes, you obtain the convolution at all image positions and produce the processed image (smoothed, edge-extracted, etc.).
Why select the neighborhood centered at (u,v)? Because to compute the convolution at (u,v) with a 3x3 kernel, you must select the 3x3 patch in the original image whose indices sum appropriately to (u,v). Convolution mixes neighboring pixels; the kernel size determines the neighborhood range. Kernel design determines whether the output is blurrier or sharper than the original.
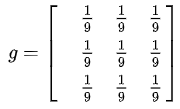
For example, this kernel averages surrounding pixels and produces a blur:
While this kernel enhances regions with large pixel value changes and extracts edges:
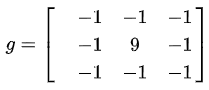
 ALLPCB
ALLPCB