Overview
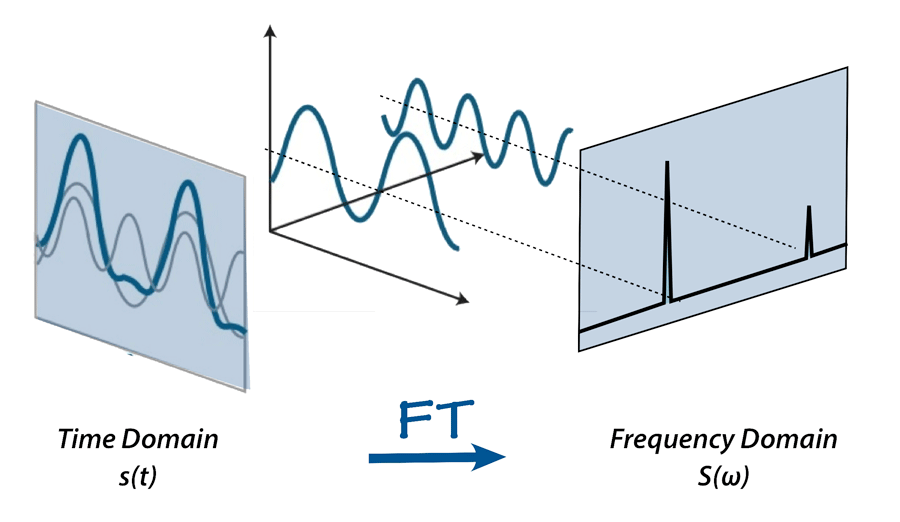
The Fourier transform is a mathematical technique that plays a key role across many scientific and engineering fields, with applications ranging from signal processing to quantum mechanics. Recently, it has found renewed relevance in the machine learning field. This article explains the basic principles of the Fourier transform and its growing role in machine learning.
The Fourier transform provides an alternative view of data by analyzing its frequency-domain representation, which is also applicable in machine learning.
Understanding the Fourier Transform
Named after the French mathematician and physicist Jean-Baptiste Joseph Fourier, the Fourier transform is an operation that decomposes a signal into its constituent frequency components. It enables analysis of a signal's frequency content and representation in the frequency domain. This transformation is especially useful for handling complex signals because it simplifies analysis of underlying patterns.
Continuous Fourier transform (CFT) and discrete Fourier transform (DFT) are two common variants. CFT applies to continuous signals, while DFT applies to discrete signals, making it more relevant for digital data and machine learning tasks. The fast Fourier transform (FFT) is an efficient algorithm for computing the DFT, which has further enabled widespread use in various applications.
FFT in Signal Processing
One of the earliest and most established applications of the Fourier transform is in signal processing. It is used for audio processing, image analysis, and data compression. For example, in audio processing the Fourier transform helps identify the different frequencies present in an audio signal, enabling tasks such as speech recognition, music classification, and noise reduction.
In image analysis, the Fourier transform can extract texture and pattern information from images. Converting an image to the frequency domain makes it easier to detect edges, shapes, and other visual features. This is important for image recognition, object detection, and image compression tasks.
FFT in Machine Learning
Machine learning focuses on developing algorithms that learn from data, and the use of the Fourier transform in this field has increased. Its applications in machine learning are diverse:
- Time series analysis: Domains such as finance, healthcare, and weather forecasting produce abundant time series data. The Fourier transform can help extract relevant features by analyzing frequency components. This is important for anomaly detection, trend analysis, and forecasting.
- Natural language processing: When text data is represented as a sequence of tokens, it can be treated as a discrete signal. Applying the Fourier transform allows analysis in the frequency domain, with potential applications in text classification, sentiment analysis, and topic modeling.
- Feature engineering: Feature engineering is a critical step in the machine learning pipeline. Converting data to the frequency domain can reveal features that are difficult to capture in the time domain, which may lead to more robust and accurate models.
- Convolutional neural networks (CNN): CNNs are a popular deep learning architecture for image analysis. The Fourier transform can be used to design filters that target specific frequency components in images. This can improve CNN performance in tasks like image classification and object recognition.
- Data augmentation: Data augmentation increases the size of training datasets. In image processing, the Fourier transform can create augmented data by modifying frequency components of images, which can improve model generalization and robustness.
Code
For time series analysis with the Fourier transform in Python, you can use numpy and matplotlib. The following is a complete Python example that uses a sample dataset and generates related plots. If the required libraries are not installed, install them first:
pip install numpy matplotlib
Below is Python code for time series analysis using the Fourier transform, including a sample dataset and plotting:
import numpy as np
import matplotlib.pyplot as plt
# Generate a sample time series dataset
# You can replace this with your own time series data
# Ensure that the data is in a NumPy array or a list
time = np.arange(0, 10, 0.01) # Time values from 0 to 10 with a step of 0.01
signal = 2 * np.sin(2 * np.pi * 1 * time) + 1 * np.sin(2 * np.pi * 2 * time)
# Plot the original time series
plt.figure(figsize=(10, 4))
plt.subplot(2, 1, 1)
plt.plot(time, signal)
plt.title('Original Time Series')
plt.xlabel('Time')
plt.ylabel('Amplitude')
# Perform the Fourier Transform
fourier_transform = np.fft.fft(signal)
frequencies = np.fft.fftfreq(len(signal), 0.01) # Frequency values (assuming a sampling interval of 0.01)
# Plot the magnitude of the Fourier Transform
plt.subplot(2, 1, 2)
plt.plot(frequencies, np.abs(fourier_transform))
plt.title('Fourier Transform')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Magnitude')
plt.xlim(0, 5) # Limit the x-axis to show frequencies up to 5 Hz
plt.tight_layout()
plt.show()
Notes on the code:
- The sample time series contains two sinusoidal components. Replace it with your own time series data as needed.
- np.fft.fft is used to perform the Fourier transform on the time series data.
- np.fft.fftfreq computes the corresponding frequency values.
- Two subplots are created: one for the original time series and one for the magnitude of the Fourier transform.
- plt.show() displays the plots.
When working with real data, replace the sample dataset with your own time series. You can adjust plotting parameters and tags according to specific requirements.
Conclusion
Originally developed for signal processing, the Fourier transform is now integrated into many machine learning workflows. Its ability to analyze and extract frequency information is valuable across time series analysis, natural language processing, feature engineering, and enhancing deep learning models. Given its versatility and adaptability, the Fourier transform remains a useful tool for researchers and practitioners aiming to gain deeper insights and develop effective algorithms.
 ALLPCB
ALLPCB