Op amp basics
Operational amplifiers are covered extensively in analog electronics texts. This article focuses on practical, application-oriented understanding to enable quick analysis of basic op amp circuits.
Basic overview
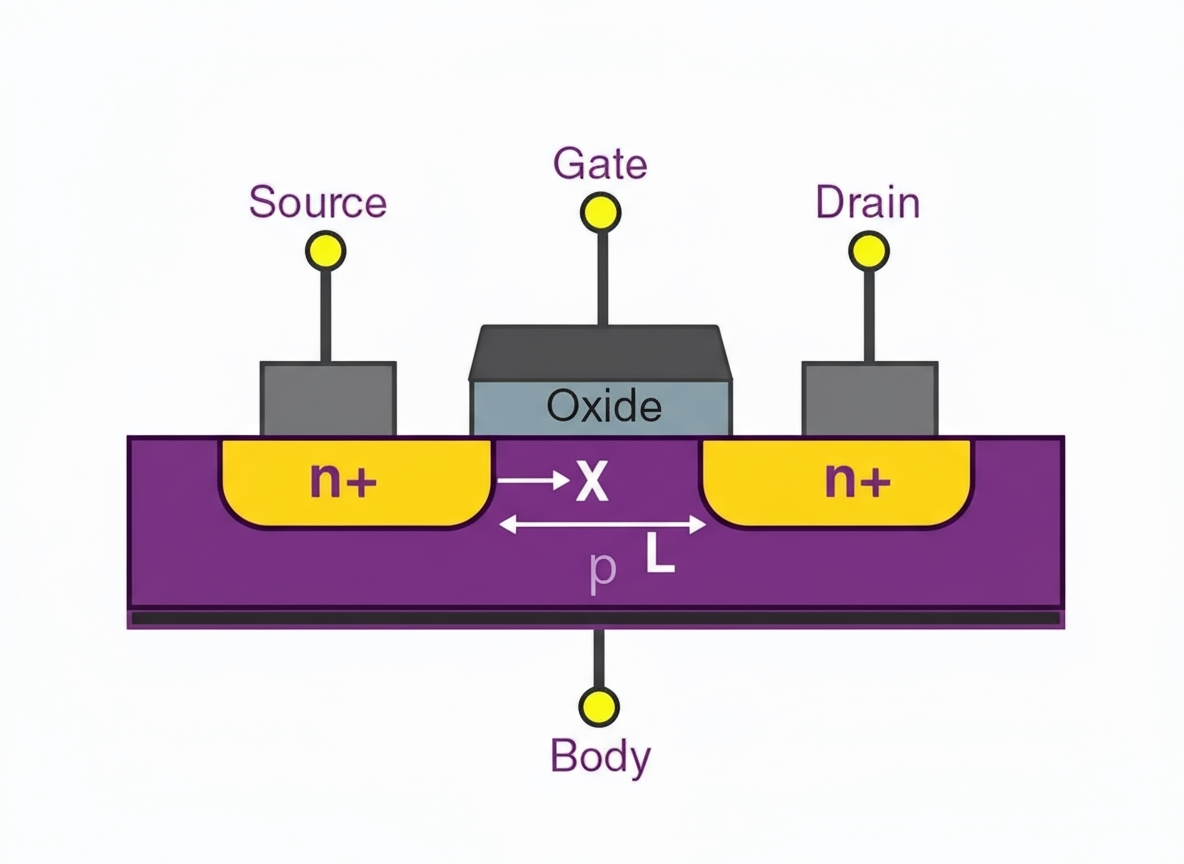
A basic op amp has two input terminals: the noninverting (+) input and the inverting (?) input, one output terminal, and two power supply pins.
Polarity behavior:
- If the input signal is applied to the inverting (?) input, the output is inverted relative to that input.
- If the input signal is applied to the noninverting (+) input, the output is in phase with that input.
- If both inputs have signals, the op amp outputs a signal corresponding to the difference, with phase determined by the larger input.
Ideal op amp assumptions: infinite input impedance, zero output impedance, infinite open-loop gain, infinite common-mode rejection ratio, and infinite bandwidth. This article uses the ideal op amp model for analysis.
Op amp currents
In the ideal model, no current flows into the input terminals. Output currents, however, do flow and are supplied by the op amp power rails. This explains why the output cannot exceed the supply voltages in magnitude.
Op amp operating characteristic
The output Vout of an op amp is given by:
Vout = A_ol * (Vin+ - Vin-)
where A_ol is the open-loop gain. For an ideal op amp A_ol → ∞, so even a tiny difference between Vin+ and Vin- drives the output to its maximum available value determined by the supply rails. This property underlies use of op amps as comparators.
Negative feedback
What is negative feedback?
Negative feedback routes a portion of the output back to the inverting input (Vin-). A simple feedback network uses a resistor from the output to Vin-:
Why use negative feedback? Circuit analysis
Without feedback, an op amp behaves like a comparator. To obtain a stable, predictable output that implements a defined mathematical relationship, negative feedback is introduced. Analysis relies on the ideal op amp assumptions: no input currents and, in a stable circuit, Vin+ ≈ Vin-.
Using Vin+ ≈ Vin- and zero input currents, the node equations give:
(0 - Vout)/R1 = Vin-/R2 → Vout = - (R1 / R2) * Vin-
This simple example shows how feedback sets a defined gain. Many standard op amp configurations can be analyzed with the same principles.
Positive feedback
Positive feedback also exists but is not analyzed here in detail. In contrast to negative feedback, positive feedback reinforces the output and input phase, increasing overall gain and enabling oscillation in appropriate circuits.
Virtual short and virtual open
Two commonly used concepts in op amp analysis are the virtual short and virtual open, both stemming from op amp characteristics.
Virtual short: In a closed-loop circuit with negative feedback, the op amp drives its output so that Vin+ ≈ Vin-. In analysis, this equality is often treated as a short circuit conceptually, hence "virtual short", though the nodes are not physically shorted.
Virtual open: With very high input impedance, op amp inputs draw no current. In analysis, inputs can be treated as open circuits, hence "virtual open".
Conclusion
- Op amp input terminals draw no current in the ideal model.
- If Vin+ < Vin-, the output will be driven to the most negative available rail; if Vin+ > Vin-, the output will be driven to the most positive available rail.
 ALLPCB
ALLPCB