Simplifying Transformer Blocks

Overview

The standard Transformer block contains multiple submodules: attention, MLP, skip connections, and normalization. Small architectural changes can slow training or even prevent convergence.

This work investigates ways to simplify the Transformer block. Combining signal propagation theory and empirical observations, the authors remove skip connections, output projection, value projection, normalization, and the serial arrangement of sub-blocks, while maintaining training speed. On both decoder-only and encoder-only models, they report a 15% reduction in trainable parameters and a 15% increase in training throughput.

Repository: bobby-he/simplified_transformers

Paper: Simplifying Transformer Blocks.

Notes and annotations:

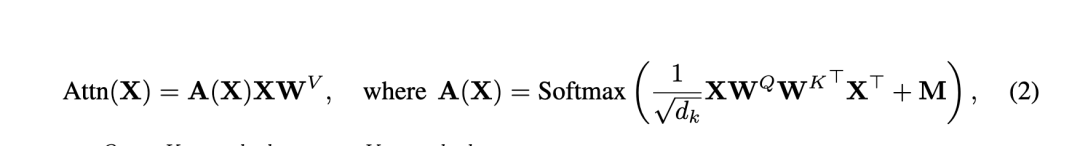
Each Transformer block is composed as shown above, and each submodule is associated with a scaling coefficient that is used in later analysis.

Removing the Skip Connection

Prior work titled "Deep Transformers without Shortcuts: Modifying Self-attention for Faithful Signal Propagation" removed residual connections and proposed a Value-Skip operation that modifies the self-attention computation. The modified attention becomes a weighted combination of the original attention operation and an identity term. Each of these two terms has its own trainable scalar, with specific initialization.

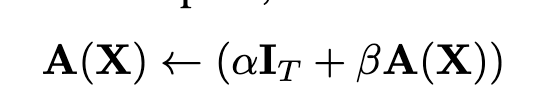
The insight is that, during early training, tokens rely more on their own features, similar to Pre-LN. Prior analysis also found that Pre-LN effectively increases the skip-branch weight and decreases the residual-branch weight to preserve signal propagation in deep networks.

Another related approach, "The Shaped Transformer: Attention Models in the Infinite Depth-and-Width Limit", introduces Shape Attention inspired by signal propagation theory and modifies the attention formula by adding a constant centering matrix C that is not learned.

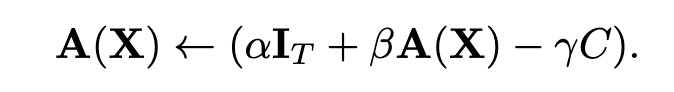
The C matrix is a constant centering matrix. It is set so that when the query-key dot product is zero, the attention A(x) equals the mask-based baseline. For causal language modeling, the mask is a lower-triangular matrix of shape (S, S) where row i has nonzero entries only in positions up to i. After softmax, the probability mass is uniformly distributed across the allowed positions, which explains the ones / arange construction used in code:

# Centered attention, from https://arxiv.org/abs/2306.17759uniform_causal_attn_mat = torch.ones((max_positions, max_positions), dtype=torch.float32) / torch.arange(1, max_positions + 1).view(-1, 1)self.register_buffer("uniform_causal_attn_mat",torch.tril(uniform_causal_attn_mat,).view(1, 1, max_positions, max_positions), persistent=False,)

For causal attention, the mask is a lower-triangular matrix where the entries in row i are nonzero only up to position i. After softmax, the probability mass is evenly split among those entries, hence the ones / arange operation. Example code:

import torchmax_positions = 32mask = torch.tril(torch.ones(max_positions, max_positions)) + torch.triu(torch.ones(max_positions, max_positions), 1) * -65536print(torch.softmax(mask, -1))

A new trainable scalar is introduced to ensure proper initialization behavior, and if these scalars are made head-wise (one per attention head), performance improves somewhat. The authors also explicitly reduce the coefficient for the MLP block:

In the paper, this coefficient is set to 0.1 for an 18-layer Transformer.

Recovering Training Speed

Introducing shape attention and removing residual connections preserves stability, but it slows convergence:

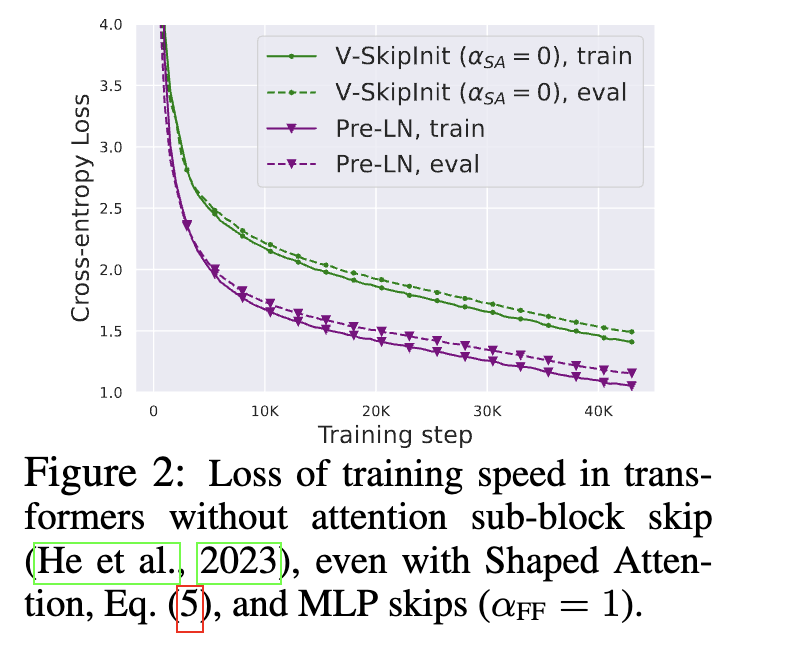
With the earlier modifications, the attention module initially reduces to matrix multiplications involving X, V projection, and the output projection. Networks without residual connections are known to train more slowly than ones with residual structure. Pre-LN reduces the residual branch contribution, which effectively lowers the learning rate and scales down parameter updates in linear layers.

This observation motivates introducing reparameterization for the V and output projection matrices.

The authors add trainable scalars to both the residual and skip branches for these two matrix operations. Empirically, most layer-wise coefficient ratios converge toward zero.

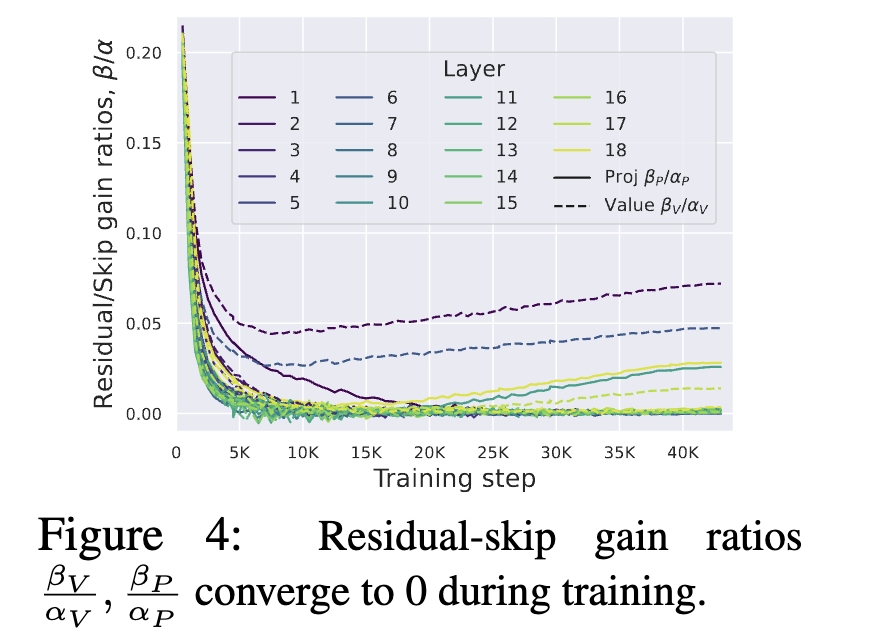
The results indicate that the two projection matrices become effectively identity matrices. Consequently, the authors remove those parameters and call the resulting attention sub-block the Simplified Attention Sub-block (SAS). Using SAS yields faster convergence than the original Pre-LN block:

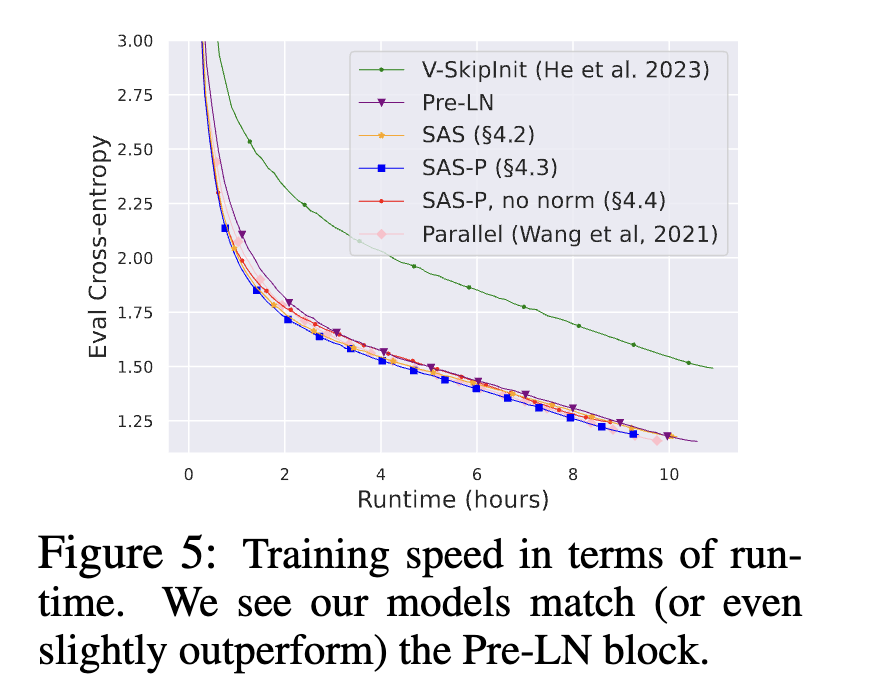
Removing the MLP Sub-block Skip Connection

The authors examine the Parallel Block introduced in GPT-J, which removes the MLP residual branch while keeping the other residual branch. The parallel arrangement computes attention and MLP in parallel and merges them with a shared residual branch:

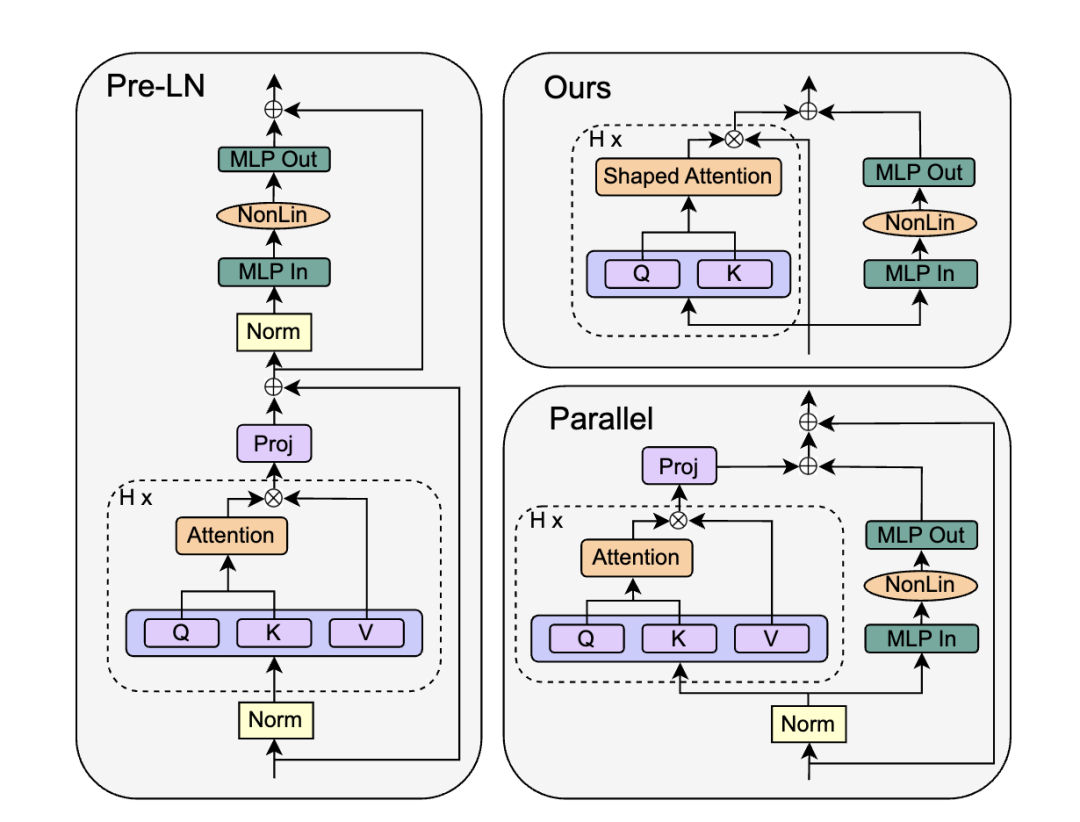
The corresponding formula is shown below:

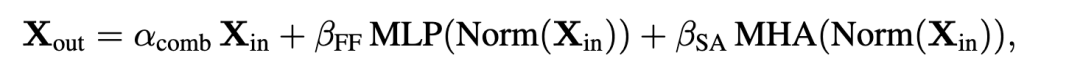
The authors replace the SAS block with a parallel form, called SAS-P. Comparing the serial and parallel implementations:

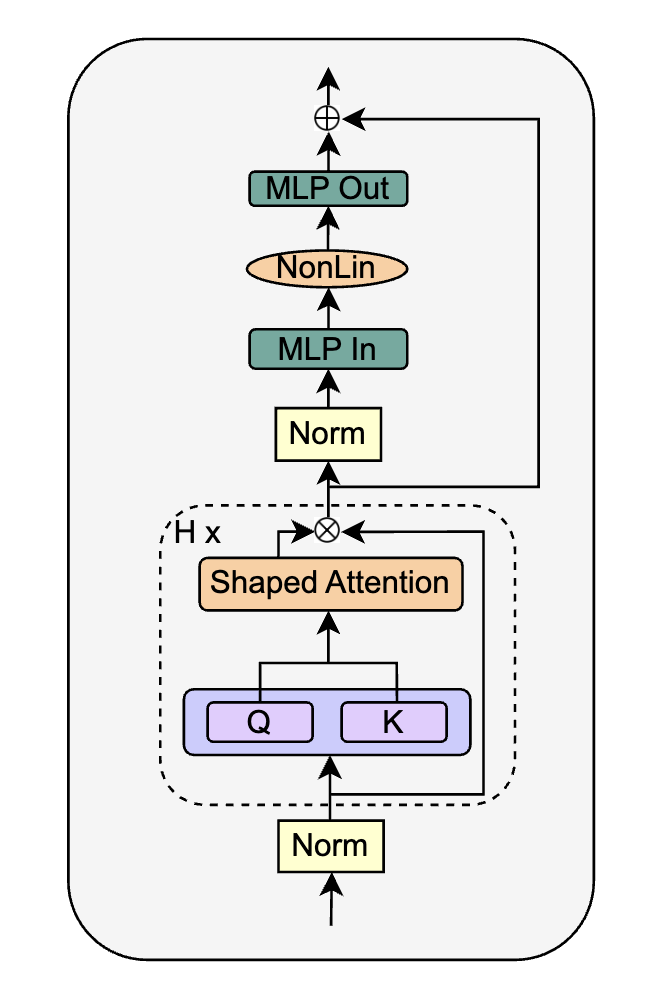
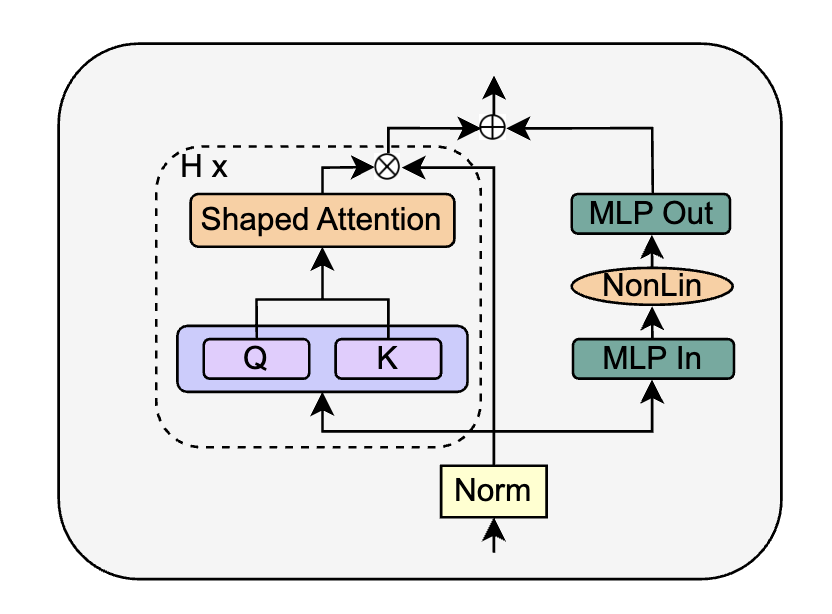
At early training steps, the attention output behaves like an identity mapping, so the serial and parallel SAS blocks are equivalent during initial training.

Removing Normalization Layers

Finally, the authors attempt removing normalization layers entirely, yielding the block below:

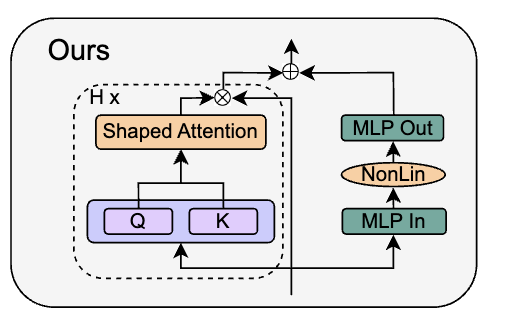
The idea is that many of the Pre-LN effects, such as increasing the skip-branch weight and decreasing the residual-branch weight, have already been achieved through the previous modifications, so normalization may be redundant.

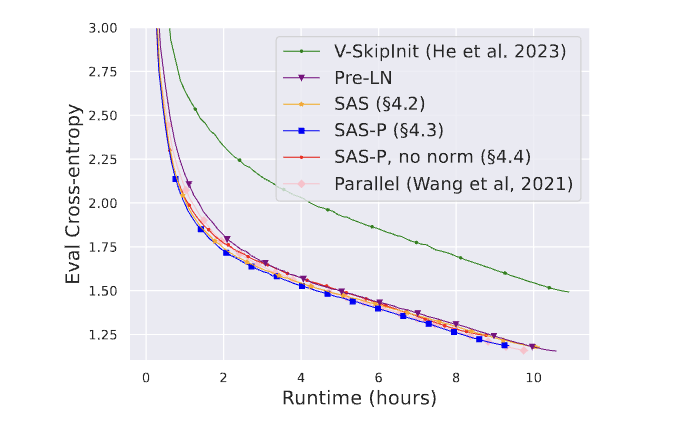
Empirical results show that removing normalization still negatively affects convergence to some extent. The authors note that normalization can accelerate convergence in practice, as observed in other large-scale transformer studies.

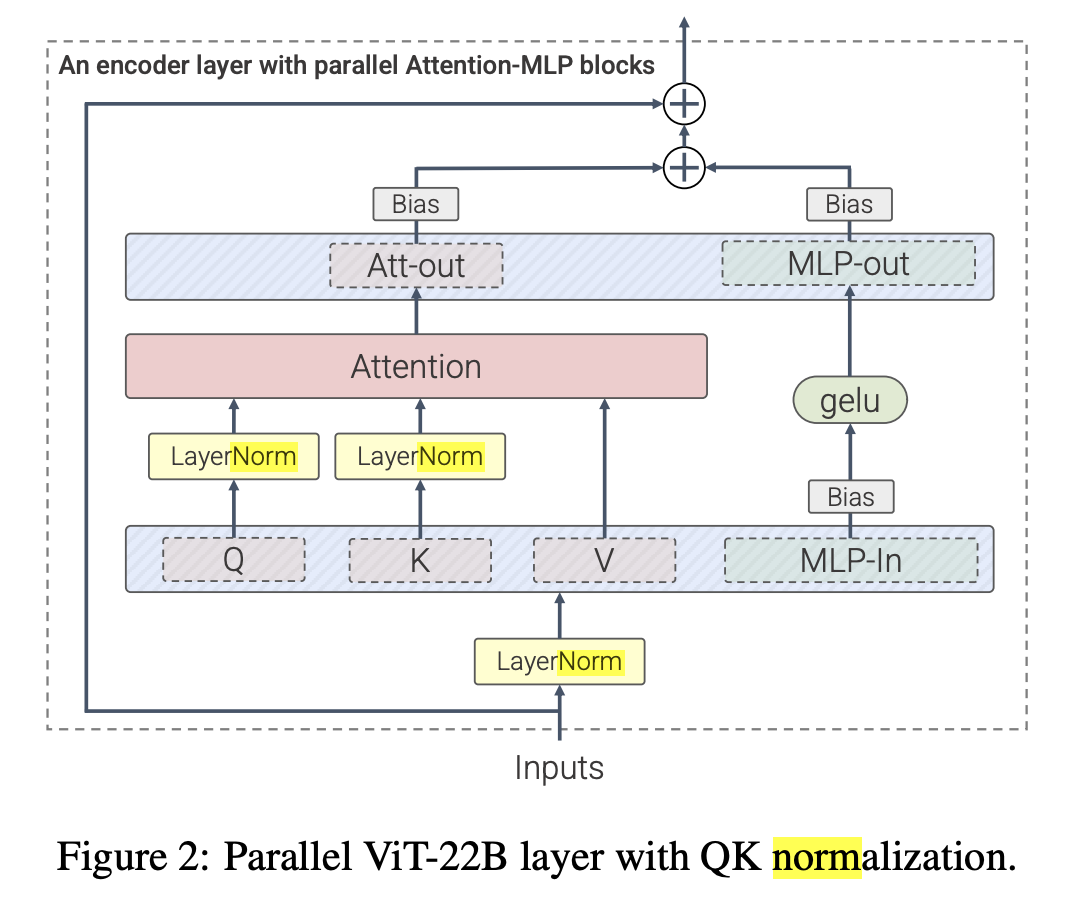
Therefore, the authors recommend retaining the Pre-LN structure in most cases:

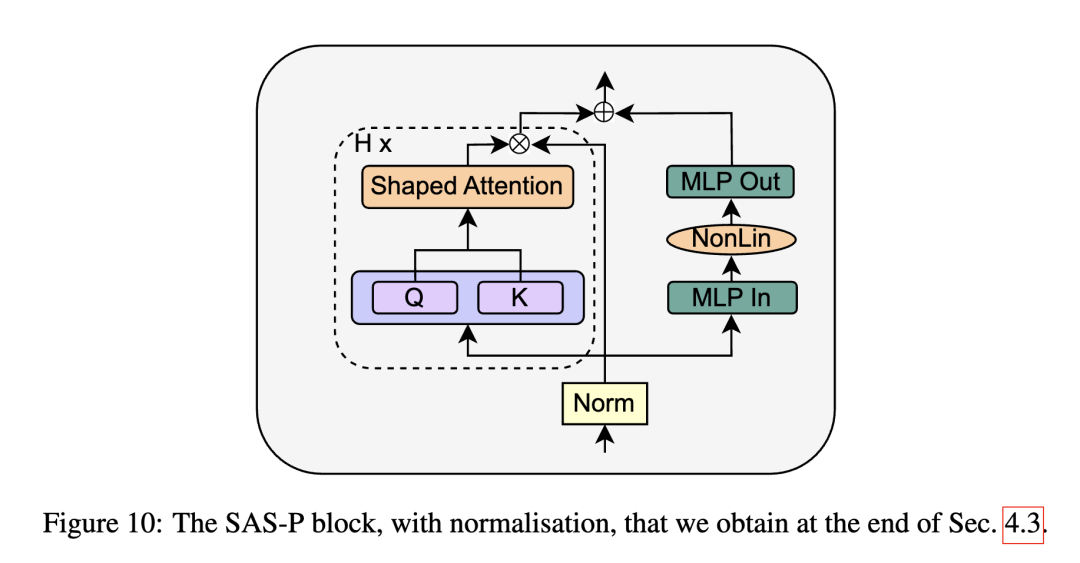
Final Experiments

The paper includes benchmarks for training throughput, model accuracy, and convergence trends:

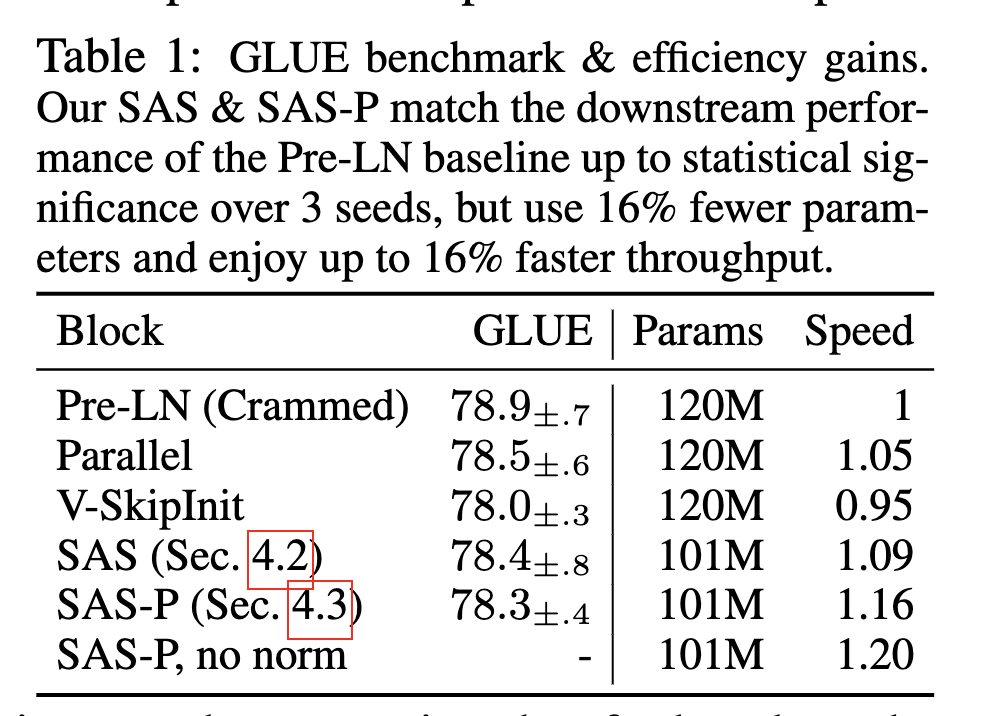
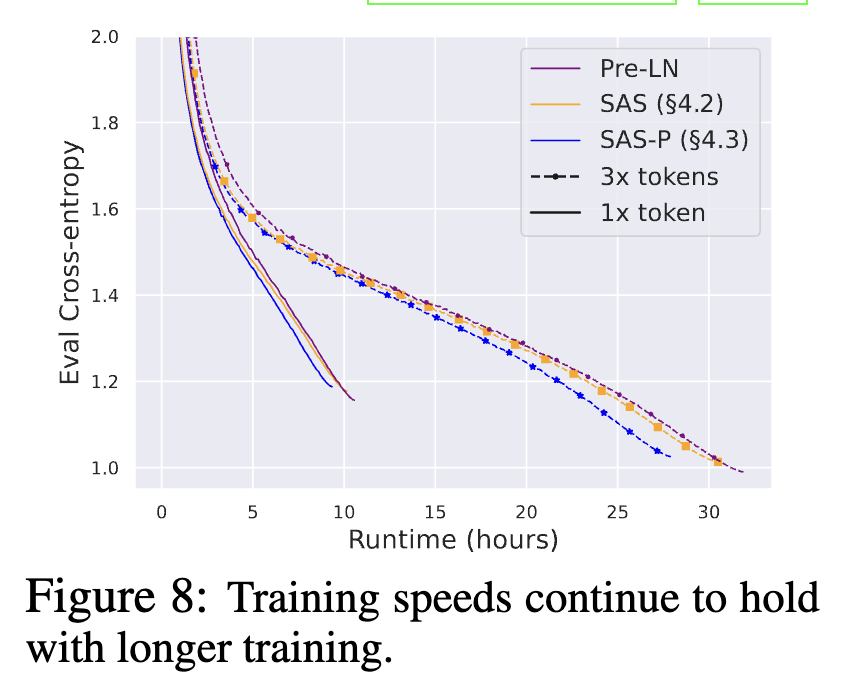
Summary

The proposed simplifications remove several parameters from the Transformer block, reducing parameter count by about 15% and improving training throughput by about 15%. The authors provide extensive experiments for each change, although some empirical findings do not fully explain underlying mechanisms, such as why layer normalization affects convergence speed.

Experimental scale is modest, and the standard Transformer block remains widely validated across scales. Further studies are needed to evaluate these simplifications at larger scales and across diverse tasks.