Resolution-Refutation Logic Reasoning for Large Language Models

1 Introduction

Natural language logic reasoning requires models to understand abstract logical relations between natural language statements and to determine the truth value of a hypothesis. This task connects natural language with abstract logical thinking, which is important for solving complex problems and cognitive reasoning. However, it remains challenging for large language models (LLMs) because they can produce incorrect intermediate reasoning steps, known as hallucinations, which can lead to incorrect final conclusions and reduce reliability. When viewed as a reasoning system, hallucinations undermine completeness: a complete reasoning system should be able to derive the truth value (True or False) of any hypothesis by applying valid inference rules contained in the system. Hallucinations prevent LLMs from arriving at conclusions via valid rules, causing incompleteness.

To reduce hallucinations and improve faithfulness, prior work has introduced chain-of-thought methods based on forward chaining or backward chaining. Forward chaining starts from known rules and facts, checking whether a rule's premises are all satisfied by given facts; if so, it derives new conclusions and repeats until no new conclusions can be drawn or the hypothesis is proved. Backward chaining starts from a hypothesis and reasons in the reverse direction to derive a set of facts that must hold, then checks whether these facts are satisfied by known facts. Introducing intermediate reasoning steps improves faithfulness of LLM-based reasoning.

However, these forward- or backward-chain methods remain inadequate in complex logic scenarios. In some cases their performance can be worse than using LLMs directly, or even worse than random guessing, because they are incomplete. Some hypotheses with definite labels may be judged Unknown. For forward chaining, completeness requires that all premises of a rule can be proven true by known facts (Condition 1). Certain cases escape that condition. For the hypothesis in Figure 1, forward chaining cannot prove it True because the prerequisite "kind people" cannot be proven from known facts, so the hypothesis is treated as Unknown. Similarly, backward chaining cannot derive a hypothesis that does not appear on any rule's right-hand side, so it is also treated as Unknown.

Inspired by symbolic-logic methods, the authors introduce a resolution-refutation reasoning paradigm that is complete under first-order logic (its inference is not constrained by Condition 1) to improve completeness, and propose the GFaiR framework. Figure 2 illustrates the resolution-refutation process. For the problem in Figure 1, using resolution rules GFaiR can perform resolution at the natural language level to derive "Everyone is not kind" from known facts. By refutation, "Bob is kind" appears among the known facts, producing a contradiction (Everyone is not kind vs. Bob is kind), thereby proving the hypothesis True. Combining resolution and refutation enables LLMs to handle more complex logical scenarios and improves generalization.

Experiments show the method achieves state-of-the-art performance in complex logic reasoning scenarios while maintaining performance on simpler tasks. GFaiR also produces more faithful reasoning traces.

2 Background

First-order logic natural language reasoning

Given a hypothesis H and a natural language theory consisting of facts and rules, the goal is to determine whether H is True, False, or Unknown using only the given theory, without external knowledge or commonsense. Each fact, rule, and hypothesis corresponds to a unique first-order logic representation. The label for H is determined by reasoning on the first-order logic representations of the facts and rules. A simple example is illustrated in the figures.

Resolution refutation

In symbolic logic, resolution refutation is a complete inference method under first-order logic. That is, for any hypothesis whose truth value under first-order semantics is True or False, resolution refutation can derive that truth value. Given a set of premises F (represented as first-order formulas) and a hypothesis Q (a first-order formula) that is True under F, the proof proceeds as follows:

• Negate Q to obtain ?Q and add it to F to form {F, ?Q}.
• Skolemize each formula in {F, ?Q} to convert them into a clause set.
• Apply the resolution principle to the clause set: iteratively resolve pairs of clauses to produce new clauses, adding intermediate conclusions back into the clause set. If an empty clause is derived, a contradiction is found, showing that Q is True.

Thus, by applying refutation to both {F, ?Q} and {F, Q} and checking for contradictions, one can determine Q's truth value: if {F, ?Q} has no contradiction but {F, Q} does, Q is False; if the reverse holds, Q is True; if neither has a contradiction, Q is Unknown.

3 Method

As shown in Figure 2, GFaiR consists of five modules: converter, forward selector, backward selector, knowledge assembler, and validator.

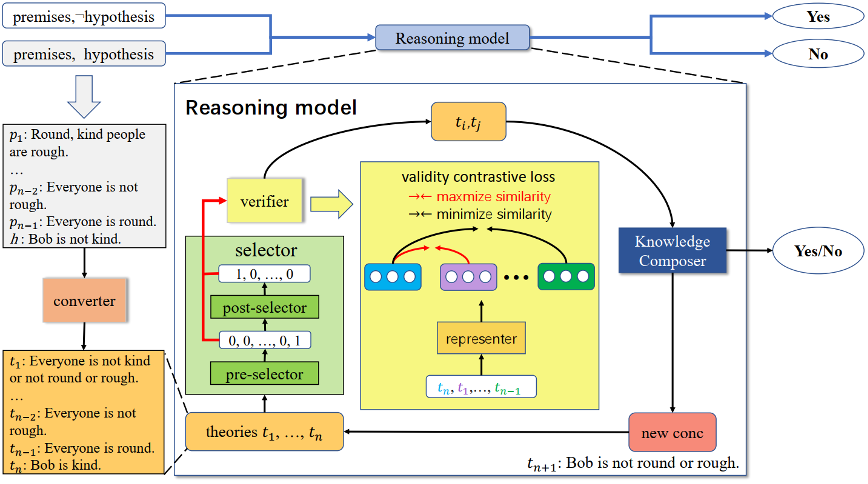
3.1 Converter

Before reasoning, a T5-based converter first negates the hypothesis for refutation. The converter then translates the given natural language theory and the hypothesis (or its negation) into natural language representations corresponding to Skolem normal form for subsequent resolution reasoning. For convenience, the converted set of natural language theories and the hypothesis (or its negation) is referred to as the theory set T, and each entry is called a theory.

3.2 Forward selector

At each reasoning step, an XLNet-based forward selector chooses one theory from T for the next resolution step.

3.3 Backward selector

After the forward selector picks a theory, an XLNet-based backward selector chooses another theory from T conditioned on the forward selector's choice. This module explicitly models the relationship between the forward-selected theory and the remaining theories, guiding the backward selector's choice.

3.4 Knowledge assembler

A T5-based knowledge assembler implicitly learns resolution rules from data and applies the learned resolution rules at the natural language level to the two theories selected by the selectors to generate a new inference.

3.5 Validator

Prior transformer-based selection modules are not sufficiently accurate for resolution-refutation and may select unrelated theory pairs, producing logically invalid inferences. If the knowledge assembler uses such unrelated pairs, it will generate invalid conclusions, causing resolution to fail and producing hallucinations. These invalid inferences may be used in later steps and lead to incorrect final results. To mitigate this, a validator based on a legality contrastive loss verifies the two selected theories to ensure they can logically produce a valid inference. This provides a guarantee for resolution reasoning and reduces hallucinations, improving faithfulness.

3.6 Inference process

At inference time, the converter transforms the given natural language theory and hypothesis (or its negation) into two theory sets, each entry represented in Skolem normal form as natural language. One set combines the theory and the hypothesis; the other combines the theory and the negated hypothesis. The reasoning model shown in Figure 2 is applied to each set to detect contradictions and determine the hypothesis truth value.

For a theory set T, the forward selector first picks a theory. Guided by the validator, the backward selector picks another theory that forms a valid theory pair; if no such theory exists, the process stops and T is considered non-contradictory. Otherwise, the knowledge assembler performs a natural language resolution on the pair to generate a new inference. If the generated inference is an empty string (corresponding to the empty clause), the process stops and T is declared contradictory. Otherwise, the new inference is added to T and the process continues.

4 Experiments

4.1 Datasets and evaluation metrics

GFaiR is trained on the RuleTaker-3ext-sat dataset and evaluated on RuleTaker-3ext-sat, Ruletaker-depth-5, and the more challenging Hard RuleTaker dataset. Because Hard RuleTaker lacks Unknown labels, Unknown examples are sampled following prior work to create a balanced dataset called Hard RuleTaker*. To assess in-domain performance on complex reasoning, Hard RuleTaker* is split into training, validation, and test sets with ratios 8.5:0.5:1, producing Hard RuleTaker**.

Evaluation metrics include: (1) Entailment accuracy (EA): accuracy of predicted hypothesis labels; (2) Full accuracy (FA): accuracy when both the predicted hypothesis label and the reasoning trace are correct.

4.2 Main experiments

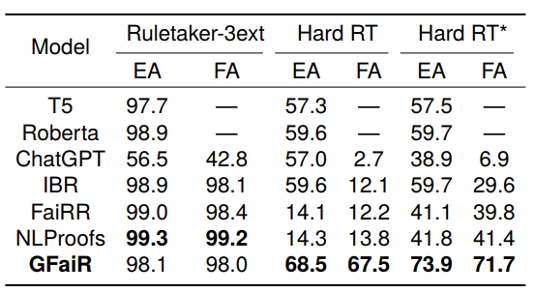
GFaiR is compared with pretrained-model baselines and stepwise reasoning methods IBR, FaiRR, and NLProofs. Results in Table 1 show that GFaiR maintains performance on simple scenarios and significantly outperforms baselines on complex scenarios, indicating improved completeness and stronger zero-shot generalization when combining resolution and refutation. The EA-to-FA gap also indicates greater faithfulness of GFaiR reasoning traces. Although NLProofs and FaiRR show smaller EA-to-FA gaps on Hard RT and Hard RT* datasets, their EA is much lower, making faithfulness comparisons less meaningful in that context.

4.3 Inference depth generalization

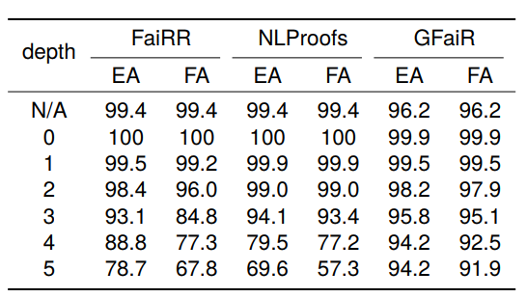
To evaluate generalization across inference depth, models are trained on RuleTaker-3ext-sat with inference depth ≤3 and tested on Ruletaker-depth-5 with depth ≤5. Table 2 shows that GFaiR's performance degrades less as depth increases. For example, when depth increases from 3 to 5, GFaiR's EA drops by 1.6%, while FaiRR and NLProofs drop by 14.4% and 24.5%, respectively, indicating stronger depth generalization for GFaiR.

4.4 In-domain performance on complex reasoning

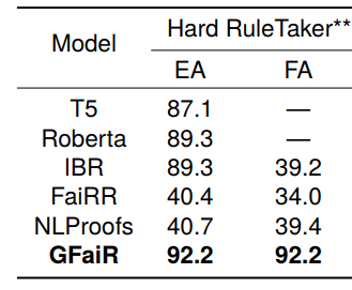
Training and testing on Hard RuleTaker** evaluates in-domain performance in complex scenarios. Table 3 shows GFaiR achieves the best results, indicating that introducing resolution-refutation improves effectiveness in complex reasoning contexts.

5 Conclusion

This work introduces GFaiR, a reasoning method that combines resolution-refutation and a validator using a legality contrastive loss to improve generalization and faithfulness in complex logic reasoning. Experiments show GFaiR attains better performance on challenging Hard RuleTaker and Hard RuleTaker* datasets.