Introduction
Computing the mean and variance of one-dimensional data is one of the most common statistical operations. Although these concepts are taught early, they have wide practical use in embedded systems:
Sensors: Fault Detection
Properly functioning sensor data should fluctuate within a limited range. Sudden shifts in the mean or abrupt changes in variance often indicate sensor faults. For example, dramatic fluctuations in a temperature sensor reading may point to poor contact.
Signal Quality Assessment
The mean and variance of GPS signal strength reflect positioning quality. Large variance indicates unstable signal, possibly due to multipath effects. Low mean indicates weak signal, possibly in obstructed environments.
Robotics Control
The variance of servo position feedback can detect stalling. The mean of motor current estimates load. The variance of wheel speed feedback can indicate surface conditions.
Battery Management
A sliding mean of voltage smooths instantaneous fluctuations. The variance of current reflects load stability. Abnormal temperature fluctuations can indicate battery issues.
All these scenarios require real-time, efficient computation of streaming statistics. Although the formulas are simple, resource limits, real-time constraints, numerical stability, and storage efficiency pose major challenges in practical systems.
Scope
This article discusses how to implement efficient mean and variance calculations under limited compute and memory. By optimizing algorithms, reducing computational complexity, using recursive formulas, and employing fixed-point arithmetic, developers can significantly reduce overhead while maintaining accuracy. These methods are well suited to IoT devices and resource-constrained embedded systems.
Fundamentals
1.1 Definitions
As known, the mean reflects the central tendency of data:
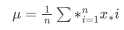
Variance reflects the data dispersion:
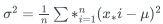
However, this naive implementation has several serious issues:
- Data storage requirements
- Computational efficiency
- Numerical stability
- Real-time constraints
Online Algorithms
Online methods, also called streaming methods, address the drawbacks of batch methods by avoiding storage of historical data. A classic online algorithm is Welford's algorithm.
Welford's algorithm, proposed by B. P. Welford in 1962, computes mean and variance online. Its core idea is to update mean and variance incrementally with each new sample without storing all past samples.
2.1 Welford Algorithm
This is a numerically stable online algorithm, particularly suitable for data streams. The algorithm uses a recursive update. When the nth sample arrives:
- Mean update
- Variance update
- Key derivation steps
Comparison and Summary
Welford's method is an online, single-pass algorithm for variance that computes variance incrementally without storing all samples. Compared with traditional batch methods, Welford reduces memory accesses and improves numerical stability. It is therefore well suited for large data streams and high-performance or resource-constrained environments.
 ALLPCB
ALLPCB