Op amp circuits
Circuits built from operational amplifiers are called op amp circuits. They appear in many forms and are a core part of learning analog electronics. They are also circuits every electronic engineer should understand. There are many op amp configurations, so is it enough to memorize them?
No. Circuits vary, and rote memorization is insufficient. The correct approach is to understand and internalize the principles.
When analyzing op amp circuits, temporarily ignore labels like noninverting, inverting, adder, subtractor, or differential input, and set aside practical device parameters such as input bias current, common-mode rejection ratio, and offset voltage. For understanding, assume an ideal amplifier. Understanding the ideal case is sufficient for most analyses.
Two simple rules handle most op amp problems. These rules are stated in textbooks as "virtual short" and "virtual open." To apply them fluently requires practice and a solid foundation.
Using these ideas, the following four classic circuits demonstrate practical analysis methods.
Virtual short and virtual open
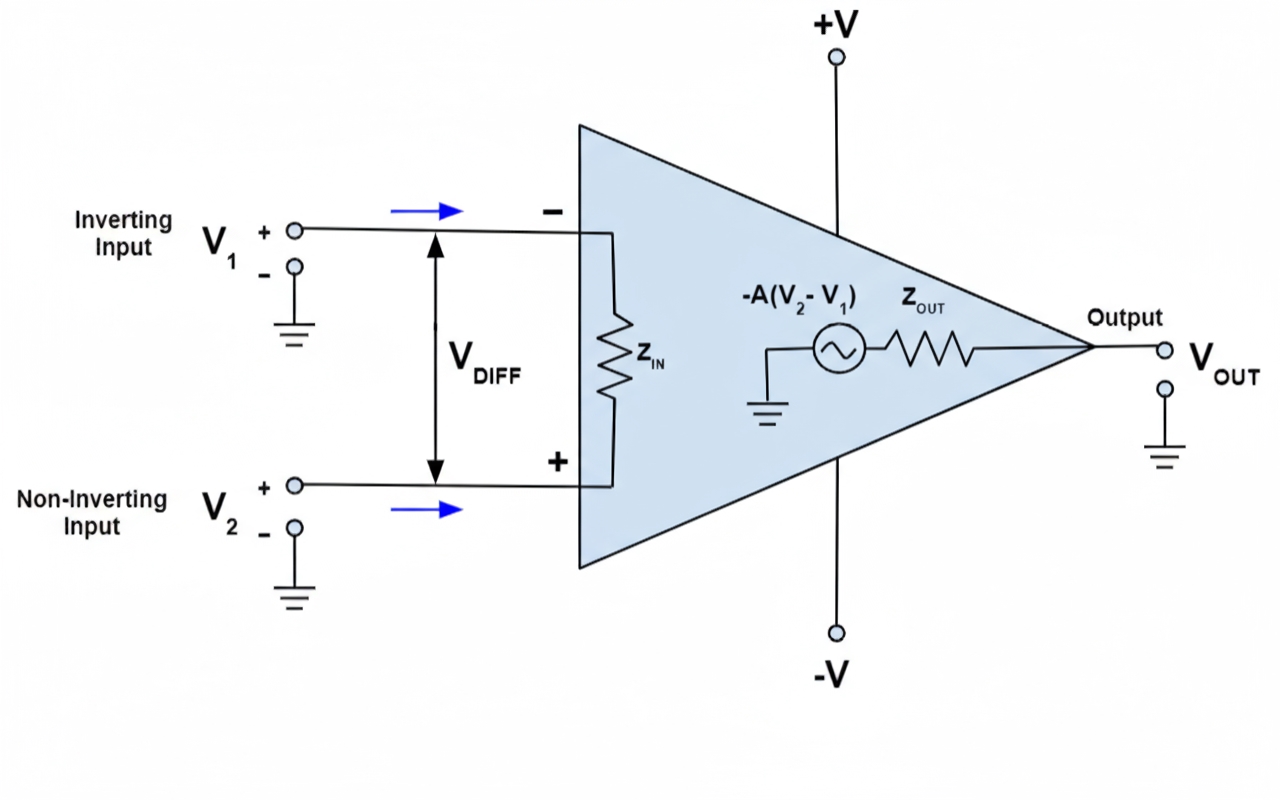
Because an op amp has a very large open-loop voltage gain, typical general-purpose op amps have open-loop gains above 80 dB. The output swing, however, is limited, typically around 10 V to 14 V. Therefore the differential input voltage is usually less than 1 mV and the two input terminals are approximately at the same potential, as if "shorted." The larger the open-loop gain, the closer the input potentials are. This reasoning explains the concept of a virtual short.
A "virtual short" means that when the op amp operates in the linear region, the two input terminals can be treated as being at the same potential. This is a notional short and the inputs are not physically shorted.
How about "virtual open"? The input resistance of an op amp is very large; typical general-purpose op amps have input resistances above 1 MΩ. The input currents are therefore often less than 1 μA, much smaller than currents in external circuitry. Consequently the input terminals can be treated as open circuits, and the larger the input resistance, the closer they behave to an open circuit.
A "virtual open" means that when the op amp operates in the linear region, the input terminals can be treated as equivalent open circuits. This is a notional open and the inputs are not physically disconnected.
With these concepts established, we analyze several examples to see how they work in practice.
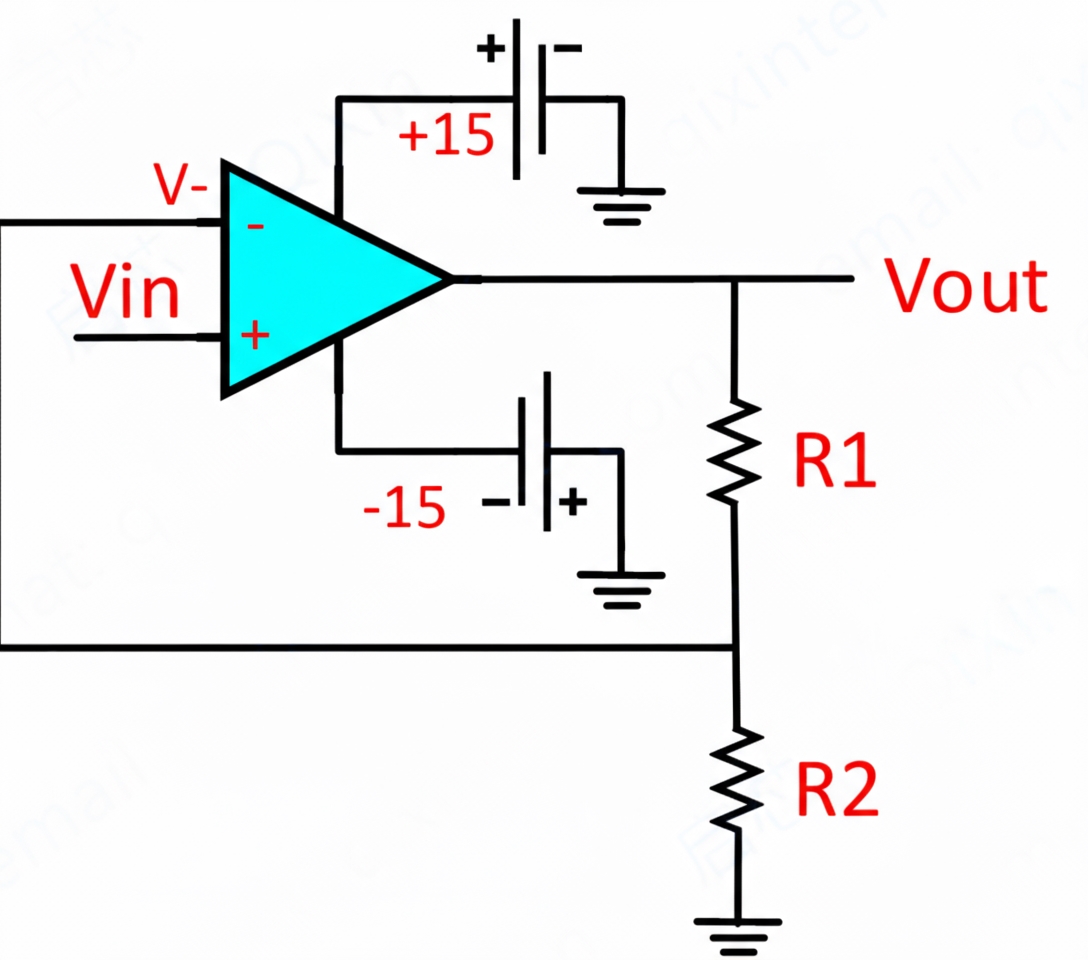
Example 1: Inverting amplifier
Analysis:
First, by the virtual short, the noninverting input is grounded at 0 V, so the inverting input is at the same potential, 0 V.
Second, by the virtual open, the inverting input draws negligible current.
Therefore R1 and R2 form a series path and the current through each resistor is equal.
Current through R1: I1 = (Vi - V-)/R1
Current through R2: I2 = (V- - Vout)/R2
V- = V+ = 0
I1 = I2
Solving yields
Vout = (-R2/R1) * Vi
This is the classic inverting proportional amplifier.
Example 2: Noninverting amplifier
Analysis:
By virtual short, Vi = V-.
By virtual open, the inverting input draws no current, so the currents through R1 and R2 are equal; call that current I.
From Ohm's law: I = Vout/(R1+R2)
Vi equals the voltage across R2, so Vi = I * R2
Therefore
Vout = Vi * (R1 + R2) / R2
This is a noninverting amplifier.
Simulation and a balanced summing circuit
An actual application is a low-frequency noise amplifier built with an OP07C, shown below. The circuit is more complex but the basic analysis principles are the same. You can try deriving the output formula yourself.
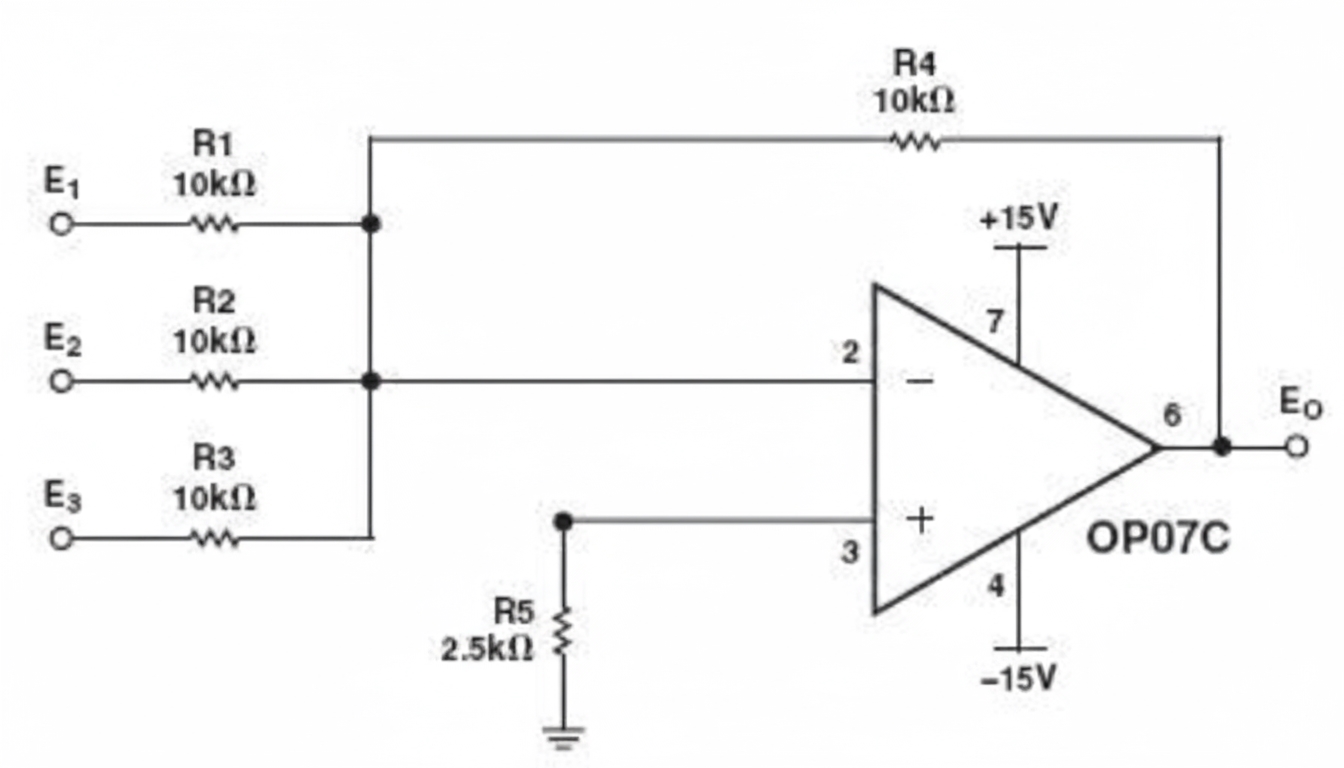
Analysis for the balanced summing circuit above:
By virtual open, no input current flows into the noninverting input, so the currents through R1 and R2 are equal; similarly the currents through R4 and R3 are equal.
Thus
(V1 - V+)/R1 = (V+ - V2)/R2
(Vout - V-)/R3 = V-/R4
By virtual short, V+ = V-.
If R1 = R2 and R3 = R4, then from the previous equations
V+ = (V1 + V2)/2
V- = Vout/2
Therefore Vout = V1 + V2
This produces another form of summing amplifier.
Conclusion
From these three examples, the basic op amp circuits can be analyzed using the same fundamental ideas. Regardless of topology or connections, mastering the principles of virtual short and virtual open allows straightforward analysis of most op amp circuits.
 ALLPCB
ALLPCB