Quantization has played a major role in accelerating neural networks — moving from 32-bit to 16-bit to 8-bit and lower. It is so important that Google is currently being sued by the creator of BF16, with claims ranging from $1.6 billion to $5.2 billion. Attention has focused on numeric formats because they have driven much of the hardware efficiency gains in AI over the past decade. Lower-precision formats help overcome the memory wall of models with tens or hundreds of billions of parameters.
This article reviews the basics of numeric formats and the current state of neural network quantization. It covers floating point versus integer, circuit design considerations, block floating point, MSFP, scaled formats, logarithmic number systems, and differences between quantization for inference and for training, including high-precision and low-precision training methods. It also discusses next steps for models that face quantization and accuracy-loss challenges.
These topics summarize the factors to consider when designing an AI chip.
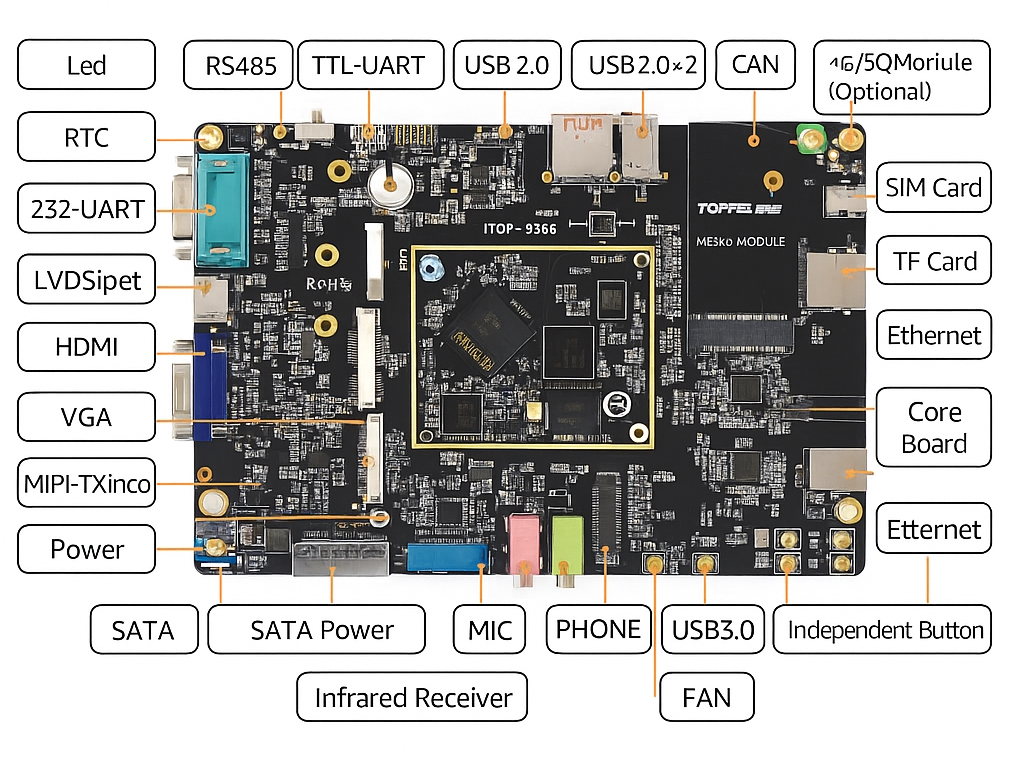
01. Matrix multiplication
Most of any modern machine learning model is matrix multiplication. In GPT-3, each layer performs large matrix multiplications: for example, one operation might multiply a (2048 x 12288) matrix by a (12288 x 49152) matrix to produce a (2048 x 49152) output matrix.
The key is how each individual element of the output matrix is computed, which reduces to a dot product of two very large vectors — in the above example, length 12288. That consists of 12288 multiplications and 12287 additions that accumulate into a single number, the output element.
Typically this is implemented by initializing an accumulator register to zero, then repeatedly performing multiply x_i * w_i and adding the result into the accumulator, with a throughput of one such operation per cycle. After roughly 12288 cycles, the accumulation for a single output element is complete. This fused multiply-add (FMA) operation is the basic compute primitive of machine learning: a chip includes thousands of FMA units arranged to reuse data efficiently, allowing many output elements to be computed in parallel and reducing the total number of cycles required.
All the numeric values above must be represented in hardware at some bit width: x_i input activations; w_i weights; p_i pairwise products; all intermediate partial sums before the final output sum; and the final outputs. In this large design space, most contemporary machine learning quantization research reduces to two goals:
- Store billions of weights accurately using as few bits as possible to reduce memory footprint and bandwidth. This depends on the numeric format used to store weights.
- Achieve good energy and area efficiency. This mainly depends on the numeric formats used for weights and activations; these goals sometimes align and sometimes conflict, which we will examine.
02. Numeric-format design goal 1: chip efficiency
Many machine learning chips are fundamentally limited by power. Although an H100 may offer up to 2,000 TFLOPS in theory, it hits power limits long before that, so FLOPS per joule is a critical metric. Given that modern training runs can now exceed 1e25 FLOPS, extremely efficient chips are needed, drawing megawatts of power over months to reach state-of-the-art results.
03. Basic number formats
First, consider the most basic numeric format used in computation: integers. Unsigned integers have obvious base-2 representations. These are called UINT, for example UINT8 (8-bit unsigned integer, range 0 to 255). Common widths are UINT8, UINT16, UINT32, and UINT64.
Negative integers require a sign. One option is sign-magnitude: put a sign bit in the most significant bit, e.g. 0011 represents +3 and 1011 represents -3. For INT8 this yields a range of -128 to 127. Sign-magnitude is intuitive but inefficient from an implementation perspective because it requires different add/subtract logic than unsigned integers.
Hardware designers instead use two's complement representation, which allows the same carry-adder circuits to handle positive, negative, and unsigned values. In unsigned int8, 255 is 11111111; adding 1 overflows to 00000000. In signed int8, the range is -128 to 127. As a trick to let INT8 and UINT8 share hardware resources, -1 can be represented as 11111111. When incremented by 1 it overflows to 00000000, representing 0 as expected. Overflow is used as a feature: values 0 to 127 map to themselves, while 128 to 255 map to -128 to -1.
04. Fixed point
We can build new numeric formats on existing integer hardware without changing the logic. These are still integers, but we interpret them as scaled values. For example, 0.025 can be stored as integer 25 if we agree that the integer represents thousandths. The full number is still an integer in hardware, but the decimal point is implicitly fixed at the third digit from the right. This is fixed point arithmetic. More generally, fixed point uses an implicit scaling factor. It is simple and often useful, but fixed-point multiplication and the required dynamic range can be limiting for some workloads.
05. Floating point
Fixed point has drawbacks, especially for multiplication when operands differ greatly in magnitude. If you need to represent values like 10^12 and 10^-12, the dynamic range is enormous. Representing such a range at uniform absolute precision would require an impractical number of bits. Instead, relative precision is usually what matters, which is the rationale behind scientific notation. Floating point adds an exponent in addition to sign and significand. The IEEE 754 standard specifies binary floating-point formats. A 32-bit float (FP32) is commonly described as (1,8,23): 1 sign bit, 8 exponent bits, and 23 significand bits.
The sign bit indicates positive or negative. The exponent is interpreted as an unsigned integer e and represents a scale factor of 2^(e-127), giving a range roughly between 2^-126 and 2^127. More exponent bits increase dynamic range; more significand bits increase relative precision. Other widths in use include FP16 (1,5,10) and BF16 (1,8,7). The trade-off is range versus precision.
06. Silicon efficiency
The numeric format used has a large impact on silicon area and power. Wider formats require more hardware for arithmetic units and wider datapaths to memory, increasing area and energy per operation.
07. Numeric-format design goal 2: accuracy
If integers are cheaper, why not use INT8 and INT16 everywhere instead of FP8 and FP16? It depends on how well those formats can represent the values that actually appear in neural networks. Each numeric format can be seen as a lookup table of representable values. A naive 2-bit format would have only four values, which is useless if the network needs values not in the table; these values would be rounded to the nearest entry, introducing error.
What is an ideal set of representable values? How small can the table be? In practice, network activations and weights often follow distributions like Gaussian or Laplace, with many values near zero and occasional outliers. For very large language models, rare extreme values can be important for the model's function. Therefore quantization schemes should allocate many representable values near zero while still accommodating outliers. One design approach is to choose a format that minimizes average absolute rounding error.
08. Logarithmic number systems
Logarithmic number systems are occasionally proposed as a way to extend 8-bit formats. They can reduce multiplicative rounding error, but they introduce other issues, such as very expensive addition circuits in the logarithmic domain.
09. Block number formats
An important observation is that elements in a tensor are often similar in magnitude to nearby elements. When a tensor element is much larger than its neighbors, the smaller neighbors contribute negligibly in a dot product. We can exploit this by sharing an exponent across multiple elements rather than using a separate floating-point exponent per element. This block-floating approach eliminates much of the redundant exponent storage.
10. Inference
Most of the above applies to both inference and training, but each has specific constraints. Inference is particularly cost and power sensitive because models are trained infrequently but deployed to millions of users. Training is more numerically demanding and includes operations that are sensitive to low precision. As a result, inference hardware typically adopts smaller, cheaper numeric formats earlier than training hardware, and there can be a large gap between training and inference formats.
11. Training
Training is more complex due to backpropagation: there are three matrix multiplications — one in the forward pass and two in the backward pass. This introduces additional numerical stability and precision requirements compared to inference.
 ALLPCB
ALLPCB